 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод хорд
|
|
В некоторых случаях несколько большей скоростью сходимости обладает метод хорд, у которого на втором этапе при выборе очередного приближения внутри отрезка, содержащего корень, учитывается величина невязки на концах отрезка: точка выбирается ближе к тому концу, где невязка меньше (но в некоторых случаях это может замедлить сходимость по сравнению с методом дихотомии).
Геометрический смысл заключается в замене кривой 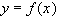 хордой. Очередное приближение находится как точка пересечения хорды с осью абсцисс.
хордой. Очередное приближение находится как точка пересечения хорды с осью абсцисс.
Если 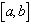 - отрезок содержащий корень, то уравнение хорды
- отрезок содержащий корень, то уравнение хорды
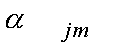 . (2)
. (2)
Для точки пересечения хорды с осью абсцисс 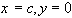 имеем
имеем
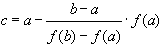 .
.
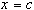 принимается за очередное приближение к корню. Далее выбирается тот из промежутков
принимается за очередное приближение к корню. Далее выбирается тот из промежутков 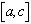 ,
, 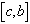 на концах которого функция имеет значения разных знаков и т. д.. При этом, если
на концах которого функция имеет значения разных знаков и т. д.. При этом, если 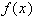 дважды непрерывно дифференцируемая функция и знак
дважды непрерывно дифференцируемая функция и знак 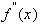 сохраняется на рассматриваемом промежутке, то полученные приближения будут сходиться к корню монотонно.
сохраняется на рассматриваемом промежутке, то полученные приближения будут сходиться к корню монотонно.
Если знаки 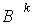 и
и 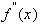 сохраняются на исходном промежутке, содержащем корень, то у всех получаемых промежутков один конец будет общим, а именно тот, на котором совпадают знаки функции и второй производной. Например, если, то последовательные приближения к корню вычисляются по формуле
сохраняются на исходном промежутке, содержащем корень, то у всех получаемых промежутков один конец будет общим, а именно тот, на котором совпадают знаки функции и второй производной. Например, если, то последовательные приближения к корню вычисляются по формуле
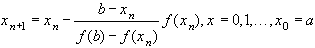 (3)
(3)
и корень принадлежит последовательности вложенных отрезков 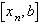
Если оставить неподвижным тот конец промежутка, где знаки 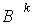 и
и 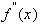 противоположны, то после вычисления
противоположны, то после вычисления 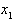 получаем промежуток не содержащий корень уравнения. Дальнейшее развитие событий зависит от поведения конкретной функции и величины промежутка. Возможна как сходимость метода (при этом соседние приближения находятся по разные стороны от корня).
получаем промежуток не содержащий корень уравнения. Дальнейшее развитие событий зависит от поведения конкретной функции и величины промежутка. Возможна как сходимость метода (при этом соседние приближения находятся по разные стороны от корня).
Рассмотрим сходимость метода хорд и оценки погрешности приближенных решений.
Пусть на исходном промежутке 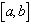 функция
функция 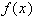 дважды дифференцируема, знаки
дважды дифференцируема, знаки 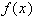 и
и 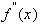 сохраняются и
сохраняются и 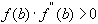
Из формулы (3) получаем
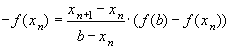 .
.
Прибавляя слева 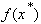 и применяя к разности
и применяя к разности 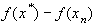 и
и
формулу конечных приращений (формулу Лагранжа), далее получаем
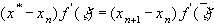 (4)
(4)
Из формулы (4) добавляя справа в скобке 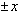 * и группируя члены, получаем
* и группируя члены, получаем
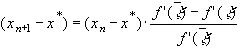 .
.
Так как знаки разностей 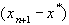 и
и 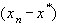 совпадают,
совпадают,
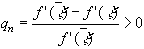 ,
,
Причем 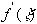 и
и 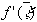 одного знака. Тогда
одного знака. Тогда 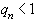
Следовательно,
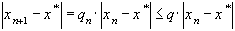 (5)
(5)
где 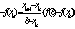
Из (5) получаем
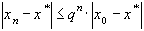
Отсюда следует, что погрешность приближенного решения 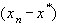 стремится к нулю при
стремится к нулю при 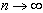 . В этом случае говорят, что метод сходится. И когда убывание погрешности приближенного решения характеризуется неравенством вида (5) говорят также, что метод имеет линейную скорость сходимости. (Сходится со скоростью геометрической прогрессии.)
. В этом случае говорят, что метод сходится. И когда убывание погрешности приближенного решения характеризуется неравенством вида (5) говорят также, что метод имеет линейную скорость сходимости. (Сходится со скоростью геометрической прогрессии.)
Из формулы (4) также следует неравенство, в котором погрешность приближенного решения оценивается через разность двух последовательных приближений
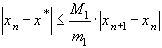 (6)
(6)
Здесь 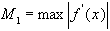 и
и 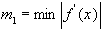 на рассматриваемом отрезке.
на рассматриваемом отрезке.
Другой вариант оценки погрешности приближенного решения через невязку дает сама формула конечных приращений
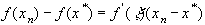
Отсюда (с учетом, что 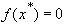 ) получаем
) получаем
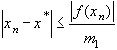 (7)
(7)
Фомы (6) и (7) позволяют установить, что для получения приближенного решения с заданной точностью (т.е. такого 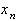 , для которого
, для которого 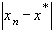 будет меньше заданного числа
будет меньше заданного числа 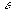 ) достаточно выполнить такое количество итераций
) достаточно выполнить такое количество итераций 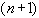 , после которого будет выполнено хотя-бы одно из условий
, после которого будет выполнено хотя-бы одно из условий
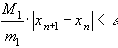 или
или 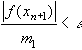
Дата публикования: 2014-11-18; Прочитано: 936 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
