Довірчі інтервали для математичного очікування

Розглянемо приклад визначення довірчих інтервалів для математичного очікування (при невідомій дисперсії) і дисперсії (при невідомому математичному очікуванні), якщо задана вибірка випадкової величини об'ємом 10 значень. Фрагмент робочого документа Mathcad має вигляд:

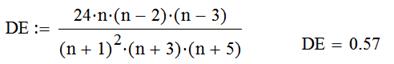
Якщо та , то розподілення випадкової величини можна вважати нормальним.

Для наведеної вибірки випадкової величини ці співвідношення виконуються, тому наближено будемо вважати розподілення нормальним.

Виберемо рівень значущості .

Тоді

95%-й довірчий інтервал для математичного сподівання

95%-й довірчий інтервал для дисперсії

Зауваження: при вирішенні прикладу були використані функції qt(p,d) і qchisq(p,d). Функція qt(p,d) вибирає по заданій вірогідності p=0,95 і числу мір свободи d =n -1 значення критерію Стьюдента.

Функція qchisq(p,d) вибирає з таблиці χ²-розподілу значення і . Тут d – число мір свободи, а, , де α – рівень значущості.