Физические и технологические основы наноэлектроники

2.1. Фундаментальные явления, лежащие в основе

функционирования наноэлектронных приборов

Наноэлектроника – это область науки и техники, занимающаяся созданием, исследованием и применением электронных приборов с нанометровыми (1 – 100 нм) размерами элементов. В основе функционирования таких приборов лежат квантоворазмерные эффекты.

Размерный эффект – зависимость свойств тела от его размера. Этот эффект возникает, если протяженность тела, по крайней мере в одном направлении, становится сравнимой с некоторой критической величиной ℓ_к .

Для классических размерных эффектов ℓ_к – классическая величина, например, диффузионная длина, длина свободного пробега электронов и т.д.

К числу фундаментальных физических явлений, определяющих поведение подвижных носителей заряда (электронов и дырок) в наноразмерных структурах, относятся: квантовое ограничение, баллистический транспорт и квантовая интерференция, а также туннелирование. Совокупность физических явлений, имеющих место в наноразмерных структурах, принято называть квантоворазмерными эффектами. Все эти эффекты есть проявление квантовомеханического (волнового) характера поведения носителей заряда в пространственных областях нанометрового масштаба.

Квантовые размерные эффекты (в электронных структурах) имеют место тогда, когда роль критической длины ℓ_к играет существенно квантовая характеристика – длина волны де Бройля λ для электронов, т.е. когда размер структуры хотя бы в одном измерении имеет порядок λ. При выполнении этого условия квантово-механические явления в наноструктурах становятся доминирующими, что и определяет их специфические электронные, оптические, магнитные и другие свойства, используемые в электронных приборах.

В связи с введением критерия (длины волны де Бройля), представляет интерес оценка линейных размеров наноструктур для разных материалов.

Длина волны де Бройля для электрона, движущегося в кристалле со скоростью ( << c – скорость света), определяется по формуле:

λ = ,

где - эффективная масса электрона; Е_кин= - его кинетическая энергия.

Рассмотрим свободные электроны в металлах. Если температура низкая, то свободными можно считать только электроны с энергиями вблизи уровня Ферми. В среднем энергия Ферми Е_F для металлов ~5 эВ. Поэтому для свободных электронов в металлах имеем Е_кин Е_F 5 эВ = 8·10^-19 Дж.

В металлах эффективная масса m^* m₀, где m₀= 9,1·10^{-31 кг – масса покоя электрона. Подставив величины Е}_кин и m^* в формулу для λ, получим λ 0,55 нм – порядок размера постоянной кристаллической решётки.

В полупроводниках энергия свободных электронов Е_кин kТ = 0,026 эВ (при комнатной температуре). Эффективная масса электрона в различных полупроводниковых материалах изменяется в широких пределах. Например, для кремния m^*= 0,92m₀, для GaAs m^*= 0,068m₀. Расчёт показывает, что для этих материалов длина волны де Бройля 8 и 30 нм, соответственно.

Так как длина волны де Бройля для свободных электронов в полупроводниках значительно больше, чем в металлах, то квантоворазмерные эффекты технологически легче осуществить в полупроводниковых структурах. Кроме того, полупроводники можно легировать и таким путём создавать p-n переходы, что необходимо для электронных приборов. Поэтому исследование квантоворазмерных эффектов и формирование наноструктур для применения в электронике проводится преимущественно в полупроводниковых материалах.

2.2. Классификация низкоразмерных объектов

Низкоразмерными структурами называют структуры, у которых, по крайней мере, один размер равен нулю. В этой связи различают двумерные, одномерные и нульмерные структуры. Такое определение носит, конечно, условный характер, поскольку реальный физический мир состоит из трёхмерных объектов. Например, толщина плоскости, сконструированной из атомов (моноатомный слой), не равна нулю, а равна диаметру одного атома, что составляет ~ 10^{-10 м. Нужно понимать, что двумерные, одномерные и нульмерные физические структуры не являются таковыми в строгом геометрическом смысле, а называются так лишь потому, что их размер в одном, двух или трех направлениях меньше определённого «критического» значения, ниже которого физические свойства структуры в этом направлении (направлениях) становятся существенно отличными от свойств объёмного (трёхмерного) материала, из которого данная структура изготовлена. Как отмечалось в п.2.1, такой «критической» величиной для полупроводниковых наноструктур является длина волны де Бройля, которая по порядку величины составляет несколько нанометров. В низкоразмерных системах свободные носители заряда локализованы в одном, двух или во всех трёх координатных направлениях в области с размерами порядка дебройлевской длины волны носителей. При этом, как уже отмечалось, вступают в силу законы квантовой механики и происходит изменение наиболее фундаментальной характеристики электронной системы – её энергетического спектра. Спектр становится дискретным для движения вдоль координаты, по которой ограничено движении.}

Ограничение движения электронов (дырок) в низкоразмерной структуре, приводящее (вследствие их квантово-волновой природы) к дискретности энергий разрешённых состояний, называется квантовым ограничением.

Как отмечалось выше, в твердых телах квантовое ограничение может быть реализовано в трёх пространственных направлениях. Количество направлений, в которых эффект квантового ограничения отсутствует, используется в качестве критерия для классификации элементарных низкоразмерных структур по трём группам: квантовые плёнки (ямы), квантовые шнуры (нити, проволоки) и квантовые точки. Ниже мы рассмотрим геометрические особенности строения простейших низкоразмерных объектов и особенности движения электронов в таких структурах. Схематически они показаны на рис.2.1.

2.2.1. Квантовая яма

Квантовая яма (плёнка) представляет собой двумерную (2D) структуру, в которой квантовое ограничение действует только в одном направлении – перпендикулярно яме (направление z на рис.2.1). Геометрически это тонкий слой (плёнка) кристалла, толщина которого d соизмерима с длиной волны де Бройля (d ~ λ) для носителей заряда. Электроны в квантовых плёнках обычно называют двумерным (или 2D) электронным газом. Носители заряда в квантовых плёнках могут свободно двигаться в плоскости xy, однако их движение в направлении оси z ограничено отрезком d_z. Двигаясь в направлении оси z, электрон не способен покинуть слой, т.к. его энергия теплового движения (~0,026 эВ при комнатной температуре) значительно меньше той энергии, которой он обладал бы проникнув в соседние области (~ несколько эВ). Поэтому движение электрона в направлении z можно рассматривать как движение в одномерной бесконечно глубокой прямоугольной яме шириной d_z.

2.2.2. Квантовая нить

Квантовая нить (шнур, проволока) – это одномерная (1D) структура.

В отличие от квантовой плёнки, она имеет не один, а два нанометровых размера, в направлении которых и действует эффект квантового ограничения. Носители заряда могут свободно двигаться только в одном направлении – вдоль оси проволоки. Движение электронов ограничено вдоль осей y и z размерами d_y и d_z, соответственно и не ограничено вдоль оси x (рис.2.1). Сечение квантовой проволоки может быть и иным, чем это изображено на рис.2.1. Потенциальная яма для свободных электронов в квантовой нити двумерная.

2.2.3. Квантовая точка

Квантовая точка – это нульмерный (0D) объект. Движение носителей заряда в такой структуре ограничено во всех трёх направлениях размерами d_x,d_y,d_z (рис.2.1). Форма квантовой точки может отличаться от кубической. Потенциальная яма для квантовой точки трёхмерная и напоминает потенциальную яму для изолированного атома. В этой связи, квантовые точки иногда называют «искусственными атомами».

2.3. Влияние квантового ограничения на энергетический

спектр и плотность состояния электронов

2.3.1 Введение

Энергетический спектр электронов и плотность квантовых состояний – важнейшие характеристики объекта, определяющие его электронные свойства и возможности применения в определённых типах приборов.

Энергетический спектр – это совокупность возможных значений энергии E частицы в данных условиях. Если энергия квантуется, то энергетический спектр называется дискретным (квантовым); если может принимать непрерывный ряд значений – спектр называется сплошным (непрерывным).

Плотность состояний n(E) - это число квантовых состояний электронов на единицу объёма, площади или длины (в зависимости от размерности объекта), отнесённое к единичному интервалу энергий. Согласно этому определению, плотность состояний равна

n(Е) = ,

где - число состояний в интервале энергий от Е до Е+dE. Значение плотности состояний n(E) и вероятности их заполнения электронами f(E) позволяет установить распределение электронов рассматриваемой системы по квантовым состояниям и описать электрические, оптические и некоторые другие свойства системы. Электроны обладают полученным спином. Поэтому вероятность заполнения ими квантовых состояний определяется статистикой Ферми-Дирака и подчиняется принципу Паули.

2.3.2. Энергетический спектр и плотность состояний

3D –электронного газа (неограниченный кристалл)

Свободный электрон, движущийся в трёхмерной системе (3D), имеет кинетическую энергию:

Е = ,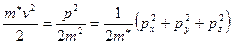

где - пространственные компоненты его импульса. Учитывая волновые свойства электрона и взаимосвязь Р = kħ, выражению для кинетической энергии можно придать вид:

Е = ,

где - приведённая постоянная Планка (); - пространственные компоненты волнового вектора.

В пределах зоны проводимости величина Е может принимать практически непрерывный ряд значений. Расстояние между соседними уровнями в энергетической зоне ~10^-22 эВ. Зависимость Е от составляющихволнового вектора (), вблизи дна зоны проводимости представлена на рис.2.1. Плотность электронных состояний определяется по формуле:

n_3D = .

Плотность состояний мала у дна зоны (откуда начинается отсчёт Е) и увеличивается пропорционально . В пределах одной энергетической зоны функции Е и n(Е) непрерывны (см.рис.2.1). Поэтому электронные свойства неограниченного кристалла под влиянием внешних воздействий (например, электрического поля) изменяются непрерывно.

2.3.3. Энергетический спектр и плотность состояний

2D – электронного газа (квантовая яма)

Как уже отмечалось ранее, в низкоразмерной структуре свободное движение электрона ограничено, по крайней мере, в одном направлении. Пусть, например, вдоль оси x имеется бесконечно глубокая потенциальная яма, в которой находится электрон. Если ширина ямы равна d, то в области 0<x<d электрон имеет нулевую потенциальную энергию. Бесконечно высокий потенциальный барьер делает невозможным нахождение электрона за границами ямы. Из решения квантовой задачи о поведении электрона в глубокой одномерной потенциальной яме с вертикальными стенками вытекает, что состояние электрона описывается гармонической волновой функцией: ψ_n(х) = ,

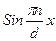где n = 1,2,3,… Фактически между стенками ямы устанавливаются электронные волны с длиной волны λ, определяемой соотношением λ_n = 2d/n (n = 1,2,3,…). Соответствующие разрешённые значения волнового вектора дискретны и равны k_n = 2π/λ_n = nπ/d. Как следствие, энергии разрешенных энергетических состояний электрона в яме тоже оказываются дискретными. Энергетический спектр определяется по формуле:

Е_n = = (2.2)

Целое число n является квантовым числом, обозначающим квантовое состояние. Таким образом, электрон, помещенный в ограниченную область пространства, может занимать только дискретные энергетические уровни. Самое низкое состояние (n = 1) имеет энергию:

Е₁ = ,

которая всегда больше нуля. Ненулевая минимальная энергия отличает квантово-механическую систему от классической, для которой энергия частицы, находящейся на дне потенциальной ямы, тождественно равна нулю. Кроме того, разрешённые значения энергии для электрона оказываются квантованными и пропорциональны n² (см. (2.2.)).

Вернёмся к квантовой яме (плёнке). Выше мы отмечали, что носители заряда в таких структурах могут двигаться в плоскости xy, а вдоль оси z их движение ограничено толщиной плёнки d_z. Их энергия складывается из суммы квантованных значений (2.2.), определяемых эффектом квантового ограничения в направлении z, и непрерывных составляющих в направлениях

x и y: Е_n = .

Следовательно, энергетический спектр электрона в квантовой яме дискретно-непрерывный.

В k-пространстве энергетическая диаграмма квантовой ямы (плёнки) представляет собой семейство параболических зон, которые, перекрываясь, образуют подзоны (см.рис.2.1).

Зависимость плотности состояний от энергии в квантовой яме имеет ступенчатый вид и определяется по формуле:

n_2D(E) = Θ(E – E_i), i = 1,2,…, где Θ(Е – Е_i) – ступенчатая функция.

Электроны в квантовых ямах (плёнках) обычно называют двумерным электронным газом (2DEG).

2.3.4. Энергетический спектр и плотность состояний

1D- электронного газа (квантовая нить)

Квантовая нить (шнур, проволока) – это одномерная (1D) структура. В отличие от квантовых плёнок, она имеет не один, а два нанометровых размера в направлении которых и действует эффект квантового ограничения.

Как уже отмечалось выше, носители заряда могут свободно двигаться только в одном направлении – вдоль оси х (см.рис.2.1). Согласно изложенному выше, энергия электрона, связанная с движением вдоль осей y и z, должна квантоваться, как в одномерных потенциальных ямах шириной d_y и d_z. Полная энергия электрона равна: ,

где n₁ = 1,2,3,…; n₂ = 1,2,3,... Положение каждого из дискретных уровней энергии зависит от двух квантовых чисел n₁ и n₂, а также от величин d_y и d_z. Зона проводимости в квантовой нити разбивается на одномерные подзоны (см. рис.2.1). Для каждой пары дискретных уровней в направлениях квантового ограничения плотность электронных состояний в квантовой нити зависит от энергии Е по закону:

n_1D(E) = ,

где i, j = 1,2,3,…. Плотность состояний на единицу длины n_1D(Е) имеет ряд резких пиков, соответствующих дискретным уровням энергии 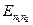(см.рис.2.1). Видно, что большинство электронов в подзоне имеет энергии вблизи соответствующего размерного уровня. Электроны в квантовых нитях называют одномерным электронным газом (1DEG).

2.3.5. Энергетический спектр и плотность состояний

OD- электронного газа (квантовая точка)

Квантовые точки – это нульмерные (OD структуры, в которых движение носителей заряда ограничено во всех трёх направлениях размерами d_x,d_y,d_z. В каждом из этих направлений энергия электрона оказывается квантованной в соответствии с формулой (2.2). Энергетический спектр электронов в квантовой точке полностью дискретен, как у отдельного атома, и определяется по формуле:

,

где n₁, n₂ и n₃ = 1,2,3,…. Величина 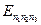зависит от трёх квантовых чисел и размеров квантовой точки.

Плотность электронных состояний представляет собой набор острых пиков, описываемых δ – функциями:

n_OD(E) = ,

где i,j,k = 1,2,3,…. График плотности состояний n_OD(Е) в квантовой точке имеет так называемый δ –образный вид (ри.2.1):

n_OD(Е) → , если Е = 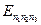(Е совпадает с размерным уровнем);

n_OD(Е) →0, если Е ≠ 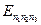(Е лежит в промежутке между размерными уровнями).

2.4. Баллистический транспорт электронов и квантование

электропроводности нанопроводников

Особенности транспорта носителей заряда в твёрдых телах во многом определяются процессами их рассеяния при движении из одной области в другую. Электрон, сталкиваясь с другим электроном или рассеиваясь на колебаниях решётки, дефектах либо границах радела, неизбежно изменяет своё состояние. Среднее расстояние, которое электрон проходит между двумя последовательными актами рассеяния, называют средней длиной свободного пробега. Различают среднюю длину свободного пробега при упругом и неупругом рассеянии. В твёрдых телах _неупр> _упр.

В макроскопических системах средняя длина свободного пробега электронов всегда намного меньше размера этих систем. В этих условиях движение электрона по проводнику носит диффузионный характер, траектория его движения – ломанная линия (рис.2.2а).

В наноструктурах условия для транспорта носителей заряда существенно отличаются от таковых в макросистемах. В структурах с размером меньше длины свободного пробега перенос носителей заряда происходит без их рассеяния. Такой перенос называется баллистическим транспортом (рис.2.2б).

Сравнивая размер наноструктуры со средней длиной свободного пробега электронов, можно предсказать основные особенности движения носителей заряда в этой наноструктуре. В металлах средняя длина свободного пробега электронов даже при низких температурах обычно не превышает 10 нм, что меньше или порядка размеров типичных наноструктур. По этой причине баллистический транспорт в металлических наноструктурах реализуется с трудом. Транспорт носителей заряда в полупроводниках характеризуется большой, до нескольких микрометров, средней длиной свободного пробега электронов. Так, например, при комнатной температуре средняя длина свободного пробега электронов при неупругом рассеянии достигает 50-100 нм в Si и около 120 нм в GaAs. Очевидно, что в полупроводниковых наноструктурах баллистический транспорт легко реализуется.

Идеальный баллистический транспорт носителей заряда в наноструктурах характеризуется универсальной баллистической проводимостью, которая не зависит от типа материала и определяется лишь фундаментальными константами. Найдём выражение и рассчитаем величину универсальной проводимости.

На рис. 2.3а изображён нанопроводник 3, помещённый между двумя металлическими контактами 1 и 2. Предположим, что температура имеет порядок нескольких градусов Кельвина и все электроны в контактах на энергетической диаграмме (см.рис. 2.3б) расположены вблизи уровней Ферми и .

Если между контактами приложить разность потенциалов U, как это показано на рис. 2.3б, то энергетические уровни металла 2 понизятся на величину eU относительно уровней металла 1. При этом 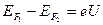. Если проводник 3 баллистический и имеет квантоворазмерное сечение (размеры сечения меньше длины волны де Бройля, т.е. проводник – квантовая проволока, то его электроны располагаются в размерных подзонах (см.рис.2.1), причём так, что большинство носителей заряда находится вблизи дна подзон. В переносе тока могут участвовать электроны подзон в интервале энергий от до . Можно показать, что каждая подзона даёт вклад в общий ток, равный: I = .

Если в интервале энергии от до находится N подзон, то ток в нанопроводнике будет равен: I₀ = , следовательно, его проводимость () определяется по формуле:

,

а сопротивление .

Таким образом, в отличие от классического проводника, сопротивление баллистической квантовой проволоки не зависит от её длины L (рис.2.3а).

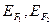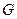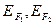Число N определяется расстоянием между подзонами, а это расстояние увеличивается с уменьшением поперечных размеров квантовой проволоки. Если постепенно уменьшать эти размеры, то из интервала энергий () будут поочерёдно по одной уходить размерные подзоны. При уходе каждой подзоны проводимость скачком уменьшается на величину Когда в интервале () не останется ни одной подзоны, проводимость 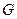обратится в ноль.

Величина называется квантом проводимости; величина кОм – квантом сопротивления. Не трудно видеть, что проводимость идеального нанопроводника в баллистическом режиме определяется только фундаментальными константами – зарядом электрона и постоянной Планка. Фактически квантование проводимости (сопротивления) есть следствие размерного квантования энергии.

2.5. Туннельный эффект. Резонансное туннелирование

Термин туннельный эффект означает перенос частицы через область (или проникновение), в которой имеется потенциальный барьер, причём высота этого барьера больше полной энергии частицы. Такой эффект невозможен с точки зрения классической механики, однако имеет место для квантовых частиц, которым, как известно, присущ корпускулярно-волновой дуализм.

Прохождение квантовых частиц через одномерные потенциальные барьеры разной высоты и ширины иллюстрирует рис.2.4.

Рис.2.4. Взаимодействие квантовой частицы с полной энергией Е со

ступенчатым барьером конечной высоты U₀, с бесконечно высоким

потенциальным барьером высотой U₀ и шириной d

Если потенциальный барьер имеет прямоугольную форму, как это показано на рис.2.4, то вероятность проникновения микрочастицы массой m с энергией Е

сквозь потенциальный барьер шириной d можно выразить простой формулой: D =D ₀ exp(- ), (2.3)

где D – коэффициент прозрачности потенциального барьера, равный отношению числа удачных попыток частицы проникнуть за барьер ∆N к общему числу таких попыток N (), величина () – носит название «дефицит» энергии частицы внутри барьера, - постоянный множитель, по величине близкий к единице. Из формулы (2.3) следует, что вероятность туннелирования уменьшается с увеличением массы частицы, ширины потенциального барьера и «дефицита» энергии. Например, коэффициент потенциального барьера толщиной d = 0,1 нм при ()=1 эВ для электрона () равен Если при тех же условиях ширина барьера d = 0,4 нм, то . Следует помнить, что для многих полупроводников эффективная масса << и коэффициент прозрачности становится заметным даже при ширине барьера несколько нм.

Туннельный эффект может происходить в двух- или многобарьерной периодической структуре (рис.2.5). Если энергия частицы совпадает с каким-либо размерным уровнем энергии в потенциальной яме, разделяющей барьеры, то вероятность прохождения частицы сквозь барьеры резко увеличивается. Такое явление называется резонансным туннелированием. Резонансное туннелирование сквозь ряд барьеров возникает только в случае, если ширина ям и барьеров имеет порядок длины волны де Бройля. В этом эффекте время прохождения электроном структуры включает, помимо времен туннелирования, время пребывания электрона в яме, разделяющей барьеры, т.е. время его жизни на резонансном уровне. Например, согласно оценке, для двойной гетероструктуры (рис.2.5), состоящей из слоёв (5 нм) - (7нм) - (5 нм) при высоте барьеров 0,2 эВ,

время туннелирования ~8∙10^-12с, т.е. такая структура может работать на частотах терагерцевого диапазона.

На основе двухбарьерной структуры созданы резонансно-туннельные диоды и транзисторы. Разработаны и находят применение многобарьерные структуры, которые называются сверхрешетками.

2.6. Перспективные полупроводниковые материалы

и структуры для наноэлектроники

2.6.1. Требования, предъявляемые к полупроводниковым материалам

Полупроводниковыми свойствами обладает широкий класс веществ. К ним принадлежат элементарные полупроводники SI и Gе, полупроводниковые соединения. А₃В₅ (GaAs, InAs, Ga и т.д.), А₂В₆ (CdTe, ZnSe), А₂В₄С₅² (ZnSiP₂), а также тройные, четверные (и более сложные) твёрдые растворы на основе соединений А₃В₅ (AlGaAs, InGaAsP и т.д.). Несмотря на обилие полупроводниковых материалов, практически в массовом производстве изделий опто- и микроэлектроники используется лишь малая часть веществ с полупроводниковыми свойствами (в основном, Si, GaAs, AlGaAs, GaAsP). Это объясняется тем, что далеко не все полупроводниковые материалы удовлетворяют высоким требованиям, предъявляемым им технологической практикой и рынком электронной продукции.

Полупроводниковые материалы, пригодные для экономически оправданного массового производства высоконадёжных приборов, должны:

· иметь высокую химическую стойкость и стабильность свойств в широком

диапазоне температур и изменений окружающей среды;

· обладать хорошей обрабатываемостью механическими, химическими и другими методами, используемыми в полупроводниковой технологии;

· давать возможность получать на их основе достаточно совершенные и чистые монокристаллические слитки и плёнки;

· допускать формирование локальных областей р- и n-типа (иметь возмож-

ность легирования);

· иметь необходимую ширину запрещенной зоны и высокую подвижность

носителей заряда;

· опираться на достаточно ёмкую сырьевую базу;

· иметь приемлемую стоимость, быть конкурентно способными на рынке.

Следует добавить, что в полупроводниковой технологии и, особенно, в нанотехнологии часто применяются компоненты полупроводниковых материалов (As, P, Zn, Ga, Al и т.д.). В этой связи, к ним предъявляются особые требования по отношению к их чистоте. Как правило, используются особо чистые вещества, содержащие ничтожное количество примесных атомов.

2.6.2. Основные технологические этапы изготовления

полупроводниковых материалов и структур на их основе

В настоящее время практически все электронные устройства бытового, военного, промышленного и научного назначения работают на интегральных микросхемах (ИМС), выполняющих множество функций. Современная технология ИМС хорошо разработана, что позволило перейти к изготовлению БИС и ГИС, и таким путём увеличить производительность и уменьшить себестоимость продукции. Очевидно, что полупроводниковая наноэлектроника, наследуя всё лучшее из технологии ИМС, также пойдёт по пути интеграции элементов и приборов, работающих на квантовых эффектах. Интегральная микро (нано) схема – это конечный продукт, для получения которого требуются основные технологические этапы полупроводникового производства.

Основными технологическими этапами изготовления полупроводниковых материалов и стурктур на их основе являются:

• получение чистого полупроводникового сырья;

• выращивание из него совершенных монокристаллических слитков с за-

данными электрофизическими свойствами;

• изготовление из слитков полупроводниковых пластин;

• получение на основе пластин (подложек) базовых полупроводниковых

структур;

• формирование в базовых структурах элементов и приборов, составляю-

щих микро (нано) схемы;

• изготовление чипов в виде отдельных законченных изделий.

Далее кратко остановимся на технологических этапах, выделяя прежде всего те задачи, которые должны быть решены по завершению определённого этапа технологического производства.

Выше мы отмечали, что к полупроводниковым материалам предъявляются жесткие требования. Этим требованиям удовлетворяют кремний, арсенид галлия и ещё ряд материалов. Однако ИМС изготавливают, в основном, на кремнии. Поэтому кремний называют базовым материалом полупроводниковой технологии. Однако ширина запрещенной зоны у Si небольшая (~1,1 эВ) и подвижность носителей заряда низкая, что не позволяет использовать Si в СВЧ приборах или для нужд оптоэлектроники. Подходящими для этих целей являются GaAs, InP и другие соединения элементов Ш и У групп таблицы Менделеева. Однако, получение монокристаллических слитков таких материалов значительно сложнее, а, в ряде случаев, просто невозможно (например, AlGaAs, CdHgTe).

Получение чистого полупроводникового сырья рассмотрим на примере кремния. В массовом производстве кремний получают восстановлением песка (SiO₂) в смеси с коксом (С) при высоких температурах. Полученный таким образом кремний называется металлургическим. Его чистота низкая и определяется, в основном, чистотой исходного кремниевого песка. Далее производится глубокая химическая очистка кремния путём превращения его в летучее соединение с последующим выделением кремния. Выделенный кремний имеет очень высокую чистоту, однако его нельзя использовать для изготовления ИМС, так как он является поликристаллическим.

Следующий этап – выращивание монокристаллических слитков с заданным типом и уровнем легирования. Это реализуется в специальных установках, работающих по методу Чохральского (метод вытягивания слитка из расплава в тигле с использованием монокристаллической затравки). В процессе выращивания из расплава происходит дополнительная (кристаллизационная) очистка материала от многих примесей (коэффициент распределения для ряда примесей много меньше единицы). Однако материал тигля (кварц, графит и т.д.) вносит в растущий кристалл свои примеси. Поэтому был разработан метод перекристаллизации кремния без использования тигля (бестигельная зонная плавка). Выращенный этим методом кремний обладает самой высокой чистотой и кристаллическим совершенством (бездефектный кремний). При необходимости слитки кремния в процессе выращивания легируются с целью получения n- или p-типа проводимости.

Монокристаллические слитки кремния обычно имеют цилиндрическую форму. Их диаметр может достигать 30 см, а высота – более 1 м.

Далее монокристаллические слитки разрезают на пластины тощиной 0,6–1,5 мм (в зависимости от диаметра), затем шлифуют до 14-го класса чистоты (зеркальная поверхность). Непосредственно перед использованием пластины обрабатывают в химических травителях.

Для изготовления ИМС используется планарная технология. Суть её в том, что все активные элементы микросхемы выполняются воздействием на полупроводниковую пластину с поверхности. При этом формирование n- и

p-областей применяют ионное легирование, загоняя примесь в кристаллическую решётку. Любые примесные атомы нарушают структуру кристалла, что снижает процент выхода готовой продукции. Процент выхода удалось значительно повысить путём формирования активных элементов в тонком эпитаксиальном слое, выращенном на подложке. Такие «сэндвичи» называются базовыми полупроводниковыми структурами.

Самый сложный и ответственный этап – формирование активных элементов (p-n переходов) в эпитаксиальном слое. Этот этап включает несколько технологических операций, основными из которых являются:

• получение диэлектрического слоя SiO₂ на кремнии путём окисления кремния в кислородосодержащей среде при высокой температуре;

• литографическая обработка поверхности с целью получения заданного рисунка микросхемы;

• легирование (диффузия, ионная имплантация) открытых областей с целью

получения n- или p-типа;

• эпитаксиальное наращивание в окнах нужных материалов;

• термическое испарение вещества в вакууме (напыление) с целью получения проводящих каналов.

Не трудно видеть, что технология ИМС на основе кремния весьма трудоёмкий и дорогостоящий процесс. Очевидно, что для перехода к наноразмерам потребуется более совершенное и дорогостоящее оборудование и квалифицированный технический персонал. Только при массовом производстве изделия наноэлектроники смогут успешно конкурировать на современном рынке.

2.6.3. Наноразмерные полупроводниковые структуры для

современной электроники

Выше отмечалось, что потенциальные возможности традиционной микроэлектроники в ближайшие годы, по-видимому, будут исчерпаны. Дальнейшее развитие электроники возможно только на базе принципиально новых физических и технологических идей. К числу физических относятся квантово-размерные эффекты, которые реализуются в наноразмерных структурах. Достижения в разработке и изготовлении наноразмерных структур различного назначения в большой степени определяются уровнем развития технологий, которые позволяют с атомной точностью получать наноструктуры необходимой конфигурации и размерности, а также методов комплексной диагностики свойств наноструктур, включая контроль в процессе изготовления (in situ) и управления на его основе технологическими процессами. Требуемая зонная структура таких наноструктур обеспечивается выбором материалов, из которых изготавливаются отдельные слои структуры («зонная инженерия»), поперечных размеров слоёв (квантовое ограничение и дискретность энергии), изменением степени связи между слоями («инженерия волновых функций»). В настоящее время, наряду с квантово-размерными планарными структурами (квантовые ямы (колодцы) и сверхрешётки на их основе), получены и исследуются одно- и нульмерные квантовые объекты (квантовые нити (проволоки) и квантовые точки), интерес к которым связан с надеждами на открытие новых физических явлений и, как следствие, на получение новых возможностей эффективного управления электронными и световыми потоками в таких структурах.

Ниже мы рассмотрим перспективы применения наноразмерных структур для создания различных полупроводниковых приборов, их зонные энергетические диаграммы, состав, размеры и кратко остановимся на способах формирования наноструктур.

Квантовые ямы (колодцы). Этим термином обозначаются системы, в которых имеется размерное квантование движения носителей заряда в одном направлении. Первоначально основные исследования квантовых ям проводились на инверсионных каналах кремниевых МОП транзисторов (рис. 2.6),

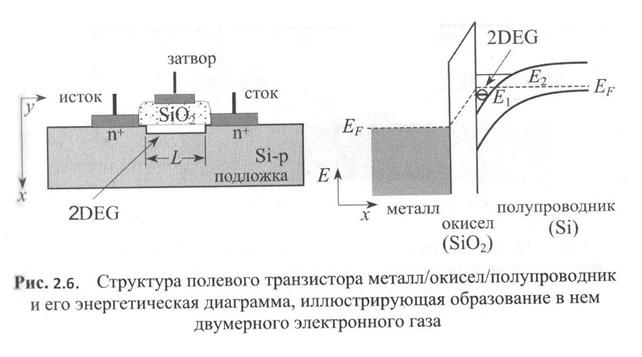
позднее и до настоящего времени широко исследуются свойства квантовых ям в полупроводниковых гетероструктурах. Лучшие результаты получены при использовании двойных гетероструктур (ДГС) в системе GaAs-AlGaAs (рис.2.7а).

Благодаря близости параметров решёток в этой системе (см.плакат) на подложке GaAs удаётся сформировать многослойные эпитаксиальные структуры разного состава с совершенными границами раздела. За создание широкого класса гетероструктур на основе твёрдого раствора AlGaAs Ж.И.Алфёрову совместно с Г.Кремером и Дж.Килби (США) в 2000 году была присуждена Нобелевская премия.

Для сравнения на рис.2.7. представлены структура (а) и упрощённая энергетическая диаграммы: классического ДГС- лазера (в) и ДГС - лазера сквантовой ямой (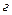). Диаграммы соответствуют прямому смещению на структуре; GaAs – узкозонный полупроводник (∆ 1,8 эВ). При прямом смещении в активный слой GaAs инжектируются электроны из n-AlGaAs и дырки из p-AlGaAs (двойная инжекция), что показано искривлёнными стрелками. Электроны и дырки не могут покинуть активный слой, т.к. он ограничен потенцииальными барьерами, и все процессы рекомбинации идут в активном активном слое. На рис. 2.7. штриховкой показаны энергетические области, занятые инжектированными зарядами. При рекомбинации испускается квант электромагнитной волны с энергией . Показатель преломления у GaAs больше, чем у AlGaAs (см.рис. 2.7б). Поэтому свет идёт по активному слою, как по волноводу, за счёт эффекта полного внутреннего отражения.

Если активный слой GaAs представляет собой квантовую яму (см.рис.2.7г),

то инжектированные при прямом смещении электроны и дырки располагаются на размерных энергетических уровнях. Рекомбинационные переходы, показанные вертикальной стрелкой, дают излучение с энергией (рис.2.7г).

Одно из преимуществ лазеров на квантовых ямах – возможность перестройки частоты излучения изменением толщины активного слоя d. Как было показано ранее, с уменьшением величины d увеличиваются расстояния от краёв зон до первых размерных уровней. Следовательно, энергия излучаемых квантов и частота увеличиваются. Другое преимущество – низкие значения порогового тока, при котором начинается лазерная генерация. Это позволило получить полупроводниковые лазеры, работающие непрерывно при комнатной температуре.

Основные физические явления в квантовых ямах: размерное квантование электронного спектра, квантовый эффект Хэлла (целочисленный и дробный), при специальном приготовлении очень высокая подвижность электронов.

Основные методы получения квантовых ям на гетероструктурах: металлоорганическая газовая эпитаксия и молекулярно-лучевая (пучковая) эпитаксия.

Приборные применения: высокочастотные полевые транзисторы с высокой подвижностью электронов, полупроводниковые гетеролазеры и светодиоды от ближнего ИК до голубого света среднего ИК диапазона, фотоприёмники среднего ИК диапазона, примесные фотоприёмники дальнего ИК дипазона, приёмники дальнего ИК диапазона на квантовом эффекте Холла, модуляторы в ближнем ИК диапазоне.

Квантовые нити (проволоки) – это системы, в которых движение носителей заряда квантовано в двух направлениях. Первые квантовые проволоки выполнялись на основе квантовых ям посредством создания потенциального рельефа с помощью двух затворов, расположенных над квантовой ямой (рис.2.8).

Основные физические явления в квантовых проволоках: квантование проводимости, сильно коррелированный электронный транспорт. Основные методы получения квантовых проволок те же, что и квантовых ям, плюс использование прецизионного травления или специальных электрических затворов. Приборных применений пока нет.

Квантовые точки – нанообъекты, в которых движение носителей заряда квантовано во всех трёх направлениях. Имеют дискретный энергетический спектр. Основные физические явления в квантовых точках: одноэлектронные и однофотонные явления. Методы получения квантовых точек те же, что и для квантовых ям, однако несколько иные режимы, если происходит спонтанный рост квантовых точек по механизму Странски-Крастанова (самоорганизация). В ряде случаев используется прецизионная литография для создания квантовых точек из квантовых ям. Для формирования квантовых точек используют полупроводниковые системы Si-Ge, GaAs-InAs, с большим различием параметров решётки (см.рис. на плакате).

Приборные применения: лазеры и светодиоды в ближнем ИК диапазоне, фотоприёмники для среднего ИК диапазона, однофотонные приёмники, однофотонные генераторы, одноэлектронные транзисторы.

Системы квантовых ям и сверхрешётки – это структуры с туннельно-

прозрачными барьерами. Основные физические явления в таких структурах: резонасное туннелирование; формирование минизонного спектра в сверхрешётках – периодических системах, содержащих много квантовых ям, разделённых туннельно-прозрачными барьерами. Методы выращивания этих структур те же, что и для квантовых ям.

Приборные применения: резонансно-туннельные диоды (генераторы и смесители в гигагерцевом и терагерцевом диапазонах); каскадные лазеры среднего и дальнего ИК диапазонов. Для изготовления сверхрешёток используются полупроводниковые материалы с близкими значениями постоянных решётки, такие как, Al_xGa_1-xAs – GaAs, In_xGa_1-xAs – GaAs, In_xGa_1-xAs – InP, ZnS – ZnSe и др.