 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Составные элементы симметрии
|
|
1. Зеркально-поворотная ось. Сочетание поворотной оси с плоскостью зеркального отражения, перпендикулярной данной оси, дает новый элемент симметрии – зеркально-поворотную ось, 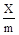 .
.
Операция симметрии представляет последовательное применение операции поворота плюс операцию зеркального отражения. Матрица представления – это произведение матриц операций поворота и отражение. Промежуточное положение после операции поворота не является симметричным; тождественным первоначальному будет конечный результат последовательного применения двух указанных элементов симметрии.
2. Инверсионная ось. Инверсионная ось симметрии – 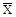 ; действие ее включает в себя операцию поворота на элементарный угол
; действие ее включает в себя операцию поворота на элементарный угол 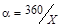 и совместно и нераздельно инверсию относительно точки, лежащей на оси.
и совместно и нераздельно инверсию относительно точки, лежащей на оси.
Все рассмотренные элементы симметрии: ось симметрии, зеркально-поворотная ось, плоскость зеркального отражения, центр симметрии, инверсионная ось действуют таким образом, что, по крайней мере, одна точка кристалла остается неподвижной. Перечисленные элементы симметрии относятся к элементам симметрии точечных групп.
При компактной записи сочетаний элементов симметрии в кристаллах используются определенные правила. Сведем наши знания об элементах симметрии в табл. 1, указав в ней правила расшифровки сочетаний элементов симметрии.
Таблица 1
| Обозначение элемента симметрии или сочетания | Расшифровка | Дополнительные сведения |
| Х, Сn | Поворотная ось | 
|
| m, sn, sv | Плоскость симметрии | 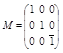 , m ^оси Z , m ^оси Z
|
Окончание табл. 1
| Обозначение элемента симметрии или сочетания | Расшифровка | Дополнительные сведения |
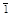 , Сi , Сi
| Центр симметрии или инверсии | 
|

| Зеркально-поворотная ось | 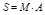
|
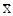
| Инверсионная ось | 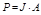
|
| Хm | Ось симметрии и параллельная ей плоскость симметрии | |

| Ось симметрии и перпендикулярная ей плоскость симметрии | |
| Х2 | Ось симметрии второго порядка, перпендикулярная оси симметрии Х-го порядка | |
| 2Х | Присутствие осей симметрии Х и второго порядка |
Рассмотрим такие сочетания элементов симметрии, как 23 и 32. В записи встречаем присутствие осей симметрии второго и третьего порядков, но во втором случае эти оси взаимно перпендикулярны. На рис. 12 показан характер расположения осей и соответственно различный вид многогранников, соответствующих каждому из этих сочетаний.
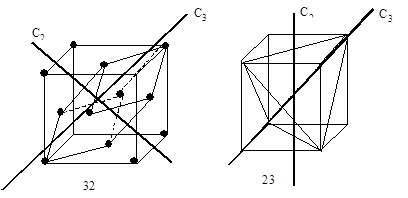 Рис. 12. Пример различных комбинаций осей 32 и 23
Рис. 12. Пример различных комбинаций осей 32 и 23
Определим симметрию гранецентрированной решетки Fm3m.
4С3 – четыре оси симметрии третьего порядка;
6m – 6 плоскостей симметрии, параллельных этим осям;
6С2 – 6 осей симметрии 2 порядка;
3С4 – 3 оси симметрии 4 порядка;
3m – 3 плоскости симметрии, перпендикулярные этим осям;
J – центр симметрии.
Симметрия решетки типа ZnS-F 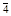 3m: 4С3, 6m, 3С4, 6С2.
3m: 4С3, 6m, 3С4, 6С2.
Дата публикования: 2014-11-18; Прочитано: 870 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
