Уравнение диффузии

Рассмотрим баланс нейтронов в единице объема dV при заданных Ф(r ), S s.

Баланс нейтронов

Рис. 9.3.1.

К изменению числа нейтронов приводят поглощение, утечка, рождение. Тогда

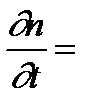рождение – утечка – поглощение.

Рождение нейтронов обусловлено источником: S(r ) -число нейтронов, рождающихся в единицу времени в единице объема вблизи r. Поглощение нейтронов определяется числом реакций в единицу времени в единице объема . Нужно найти выход реакции в элементе объёма

.

Найдем утечку нейтронов, зная вектор плотности J из закона Фика

Если известенвектор J в каждой точке поверхности элементарного объема dV, то утечка равна div J - число нейтронов, пересекающих поверхность единичного объема в единицу времени. Причем

div / D= const/= – D D Ф

где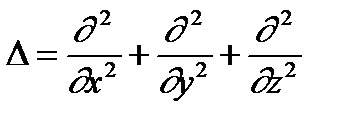

Таким образом, имеем уравнение

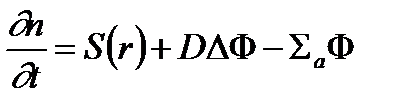
В стационарном случае

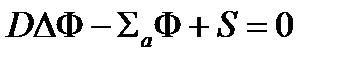
Замечания:

При выводе данных уравнений пользовались законом Фика, который справедлив, если распределение потока по координатам является линейным на расстоянии в несколько 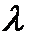. Значит, эти уравнения плохо работают вблизи границы источника. Коэффициент D здесь уже учитывает возможную несферичность рассеяния(см. ранее).

Граничные условия:

1) поток Ф нейтронов конечен и неотрицателен в области, где применимо уравнение диффузии;

2) на границе двух сред, отличающихся хотя бы одной характеристикой взаимодействия нейтронов с ядрами.

Взаимодействие нейтронов с ядрами

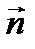
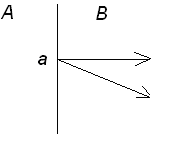
Рис. 9.4.1.

В точке а:

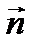- нормаль к поверхности;

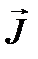- ток нейтронов.

Так как сама граница не поглощает нейтроны, то сколько нейтронов уходит из среды А, столько и приходит в среду В, т.е. проекции на нормаль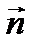

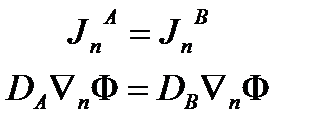
т. е. поток на границе неразрывен.

С другой стороны, при переходе через границу поток нейтронов должен быть непрерывной функцией координат, т.е.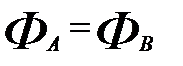

Итак, имеем условия на границе

Условия на границе

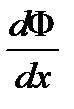
x

А

В

Рис. 9.4.2.

Условия на границе

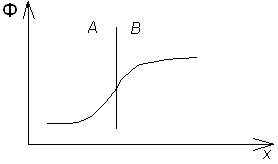
Рис. 9.4.3.

3) на границе среды с вакуумом (это условие необходимо при решении задач о конечном реакторе) нет потока внутрь среды из вакуума. Это условие можно выразить, если задать функцию Ф(r, E, W). На границе имеем:

функция Ф ( r, E, W ).

среда

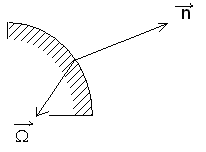
Рис. 9.4.4.

Видно, что это граничное условие нельзя записать, зная только зависимость Ф от r. Используем следующий прием: изобразим Ф (r) в плоском реакторе. Очевидно, поток на границе меньше, чем в центре активной зоны, но не равен 0, т.е. 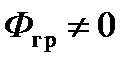. Уравнение наиболее просто решается при нулевых граничных условиях.

Поток на границе

х

Ф(х)

Фmax

Ф

α

Рис. 9.4.5.

Решение уравнения диффузии особенно просто, когда на какой-либо границе поток равен 0. Будем считать, что поток образуется в 0 не на физической, а на некоторой экстраполированной границе реактора (экстраполяция линейная).

Длина экстраполяции d – величина неопределенная, но вносящая малую поправку в уравнение диффузии. Оценка d была сделана как теоретически, так и экспериментально. Оказалось, что при d = 0,71 λ _tr наблюдается наилучшее совпадение теории с опытом.