Симетрична різниця тотожність

З умови додатковості операцій витікають слідуючі співвідношення:

~ ~

~

Основні закони логіки Буля:

1) закони ідемпотентності (самопоглинання):

2) закони комутативності:

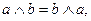
3) закони асоціативності:

4) закони дистрибутивності:

;

5) закони нуля та одиниці:

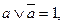
6) закони поглинання:

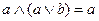
7) закони де Моргана:

8) закони склеювання:

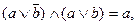
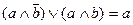
Логічну функцію, яка залежить від двох змінних можна представити слідуючим чином:

Подібна функція представлення логічних функцій має назву досконалої диз’юнктивної нормальної форми (ДДНФ).

У логіці Буля діє принцип двоїстості, який говорить: при одночасній заміні символів 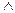на 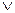, 1 на 0 усі логічні рівності залишаються у силі. Тому нашу ДДНФ можна представити трохи іншим чином:

Ця форма представлення має назву досконалої кон’юктивної нормальної форми (ДКНФ). Тут вже констітуєнти представлені не в вигляді кон’юнктів, як в ДДНФ, а в вигляді диз’юнктів. З’єднані ж ці диз’юнкти кон’юнкцієй, звідки і назва – ДКНФ.

Існує ще і третя форма – досконала поліноміальна нормальна форма (ДПНФ). Її легко можна отримати з ДДНФ шляхом заміни:

Через те, що констітуєнти не пересікаються , ми можемо записати (в ДПНФ символ кон’юнкції опускається):

.

У слідуючій таблиці приведен повний список елементарних логічних функцій від двох аргументів та в трьох досконалих формах – ДДНФ, ДКНФ та ДПНФ. Досконалі форми представлень дозволяють виразити аналітичною формулою будь-яку функцію, якщо відома її таблиця істинності:

	ДДНФ=ДКНФ=ДПНФ
~

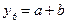
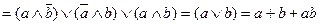
З допомогою цих формул, а також законів логіки Буля, можна доказати справедливість будь-якого логічного вираження.

Приклад: доказати тотожність

Ми знаємо, що , тоді

Приклад: використовуя операції над множинами, представити заштриховані області у вигляді компактного аналітичного вираження.

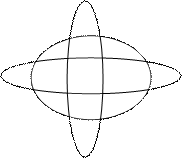Заштриховані області можна представити з допомогою чотирьох констітуєнт:

~