Свойства определителей

Изложенные ниже свойства справедливы для любого n-го порядка. Доказательства будем проводить для n=3.

1. Определитель не меняется при транспонировании, т.е. ^Т)= 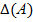. Поэтому в дальнейшем большинство свойств формулируется и доказывается для строк.

2. Если две строки определителя поменять местами, то определитель меняет знак.

3. Если все элементы какой-либо строки (или столбца) равны нулю, то определитель равен нулю.

4. Если все элементы какой-либо строки (столбца) имеют общий множитель, то его можно вынести за знак определителя.

5. Если в определителе две строки (два столбца) одинаковы или пропорциональны, то определитель равен нулю.

6.

7. Определитель не изменяется, если к элементам какой-либо строки (столбца) прибавить элементы другой строки (столбца), умноженные на одно и то же число.

8. Сумма произведений элементов любой строки (столбца) на свои алгебраические дополнения равна самому определителю. Сумма произведений любой строки (столбца) на алгебраические дополнения другой строки (столбца) равна 0.

Если нулю равны все элементы другой строки, то, поменяв ее местами с первой (что может повлиять лишь на знак определителя), мы сведем дело к предыдущему. Свойства 4), 6) читатель докажет самостоятельно, используя понятие определителя.

Док-во 5). Если поменять местами одинаковые строки, то, с одной стороны, определитель не изменится, а с другой — на основании св. 2, он поменяет знак, т. е.

Док-во 7) следует теперь из 6) и 5)

9. Определитель треугольной матрицы равен про­изведению элементов главной диагонали

Доказательство. Раскладывая по элементам 1-го стол­бца, получаем произведение ведущего элемента а₁₁ на оп­ределитель такого же вида (n-l)-ro порядка с ведущим элементом а₂₂. Раскладывая этот определитель по элемен­там 1-го столбца, имеем произведение а₂₂ на определитель такого же вида (n-2)-го порядка. Это значит, что равен произведению а₁₁*а₂₂ на этот новый определитель. Про­должая этот процесс, необходимое число раз, приходим к

равенству

a₁₁*a₂₂*a₃₃…a_nn.

Сформулируем без доказательства еще один важный факт.

квадратные матрицы одного

ТЕОРЕМА 1.1. Если А и В - порядка, то

1.3. обратная матрица. существование и структура обратной матрицы

Матрица А^-1 называется обратной к квадратной матрице А, если

А*А^-1=А^-1*А=Е.

ТЕОРЕМА 1.2. Для того чтобы матрица А имела об­ратную, необходимо и достаточно, чтобы она была невы­рожденной, т. е. чтобы (А)≠0.

ДОСТАТОЧНОСТЬ. Дано: (А)≠0• Докажем, что обратной к матрице А является матрица

Каждый из элементов главной диагонали равен опре­делителю (А), ибо представляет собой сумму произведений элементов одной из строк матрицы на свои алгебраические дополнения. Все остальные числа в результирующей мат­рице равны нулю на основании второй части свойства 8).

Поэтому,

Совершенно аналогично доказывается, что. А * А^-1= Е. Это завершает доказательство достаточности.

НЕОБХОДИМОСТЬ. Дано, что матрица А^-1 существу­ет. Надо доказать, что (А) ≠0. Допуская, что (А) = 0, мы бы получили из равенства А• А^-1 = Е, (А) • (А^-1) = Е, откуда (А)* 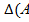^-1)=1, что невозможно, ибо левая часть этого равенства есть 0.

ПРИМЕР 4. Найти обратную к матрице

2 -1 -2

А= 3 1 -1

-2 3 4

РЕШЕНИЕ. Вычисляем алгебраические дополнения всех элементов данной матрицы:

Находим определитель матрицы А:

Теперь записываем обратную матрицу

ПРОВЕРКА:

Значит, матрица А^-1 найдена, верно.