Глава 1. Основы линейной алгебры

1 Название, цель, содержание работы.

2 Результаты выполнения работы (сохранить на дискете).

3 Письменные ответы на контрольные вопросы.

4 Выводы по работе.

Раздел II Элементы линейной алгебры

Тема: матрицы и определители

Вопросы:

1) Понятие матрицы и виды матриц

2) Квадратные матрицы и их определители

3) Свойства определителей квадратных матриц

4) Действия над матрицами

5) Обратная матрица

Учебник: И.В.Виленкин, В.М. Гробер «Высшая математика» для студентов экономических, технических, естественнонаучных специальностей вузов. Издание 2008г.

Глава 1. ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ

§1. МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ

1.1 первоначальные понятия. линейные операции над матрицами. умножение матриц

МАТРИЦЕЙ размера m*n называется прямоугольная таблица чисел

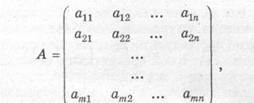
содержащая т строк и п столбцов. Каждый элемент матрицы а_ik имеет два индекса: i — номер строки и k номер столбца. Краткая форма записи матрицы:

A= (a_ik) _{m, n.}

Матрица называется КВАДРАТНОЙ порядка п, если она состоит из п строк и п столбцов.

Матрица размера 1 х п называется МАТРИЦЕЙ-СТРОКОЙ, а матрица размера m х 1 - МАТРИЦЕЙ-СТОЛБЦОМ.

НУЛЕВОЙ матрицей заданного размера называется матрица, все элементы которой равны нулю.

ТРЕУГОЛЬНОЙ матрицей га-го порядка называется квадратная матрица, все элементы которой, расположенные ниже главной диагонали, равны нулю:

Определение главной диагонали:

Главной диагональю квадратной матрицы называется её диагональ, составленная из элементов а₁₁, а₂₂, а₃₃, …, а_nn

ЕДИНИЧНОЙ называется квадратная матрица n-го порядка, у которой элементы главной диагонали равны единице, а все остальные элементы — нули: