Комплексні числа

1.Алгебраїчна форма комплексного числа.

Означення 5.3. Комплексним числом z називають символ

, (5.10)

де х і у – дійсні числа, а і – уявна одиниця, яка означається рівністю і ²=-1. При цьому х називається дійсною частиною комплексного числа z і позначається х =Re z; у – уявною частиною і позначається y= Im z.

Комплексні числа 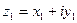і вважаються рівними, якщо відповідно рівні їх дійсні й уявні частини:

Зокрема, комплексне число =0 тоді і лише тоді, коли х =0 і у =0.

Якщо у =0, то комплексне число має вигляд . Його записуємо z = x і називатимемо дійсним числом.

Якщо х =0, , то комплексне число має вигляд або z=iy. Його називатимемо чисто уявним числом.

Два комплексні числа та , які різняться лише знаком уявної частини, називаються спряженими.

Дії над комплексними числами, заданими в алгебраїчній формі, виконуються за такими правилами:

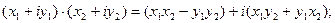
2. Геометричне зображення комплексного числа.

Комплексне число геометрично зображається точкою з координатами х, у на площині хОу. Цю площину називають комплексною площиною.

Вісь Ох називається дійсною віссю, вісь Оу – уявною віссю.

Сполучимо точку М (х; у) з початком координат. Дістанемо вектор . В окремих випадках зручно вважати вектор геометричним образом числа .

3. Тригонометрична і показникова форми комплексного числа.

Позначимо через jі r () полярні координати точки М (х; у), вважаючи початок координат полюсом, додатній напрямок осі Ох – полярною віссю. В цьому випадку справедливі співвідношення

.

Комплексне число можемо представити в тригонометричній формі

або в показниковій формі

.

Величини jі r виражаються через х і у формулами

і називаються r – модулем, j - аргументом комплексного числа .

Множення, ділення, піднесення до степеня і добування кореня для комплексних чисел, заданих в тригонометричній і показниковій формах, виконуються за такими формулами: