 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Первісна функція і невизначений інтеграл
|
|
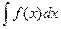
При цьому  називають підінтегральною функцією, а
називають підінтегральною функцією, а  - підінтегральним виразом.
- підінтегральним виразом.
Отже, якщо функція  є первісною функцією для функції
є первісною функцією для функції  , то
, то
 . (5.1)
. (5.1)
Знаходження невизначеного інтеграла для функції  називається інтегруванням даної функції.
називається інтегруванням даної функції.
§5.2. Властивості невизначеного інтеграла
Перша група властивостей. Послідовне виконання операцій диференціювання і інтегрування в будь-якому порядку з точністю до довільної сталої приводить до початкової функції: 

Звідси дістаємо правило перевірки того, чи правильно знайдено первісну функцію для даної функції. Для цього треба знайдену функцію продиференціювати. Якщо дістанемо підінтегральну функцію, то первісну знайдено правильно.
Друга група властивостей. Лінійні властивості інтеграла:
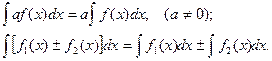
Вказівка. При доведенні сформульованих властивостей достатньо скористатись означенням первісної функції.
§5.3. Основна таблиця інтегралів
Оскільки операція інтегрування є оберненою до операції диференціювання, то можна для кожної функції (з основної таблиці похідних) написати їй відповідну первісну функцію (невизначений інтеграл). Тоді дістанемо таку таблицю інтегралів:
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 
11. 
12. 
13. 
14. 
15. 
16. 
17. 
18. 
19. 
§5.4. Метод підстановки
Усі методи інтегрування функцій зводять невизначений інтеграл до інтеграла, який є в основній таблиці інтегралів, або, як кажуть, до табличного інтеграла. Одним з найбільш сильних методів є так званий метод підстановки (метод заміни змінної). Цей метод полягає в зміні аргументу підінтегральної функції за деякою формулою, розрахованій на те, щоб інтеграл від нової змінної був простішим в обчисленні:
З’ясуємо більш детально суть методу підстановки.
Нехай треба обчислити (знайти) невизначений інтеграл
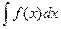 , (5.2)
, (5.2)
який не є табличним.
Змінну інтегрування х в інтегралі (5.2) замінимо деякою функцією
 , (5.3)
, (5.3)
де 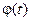 - диференційовна функція на певному проміжку, має неперервну похідну
- диференційовна функція на певному проміжку, має неперервну похідну  і обернену функцію
і обернену функцію  .
.
Знайдемо диференціал від обох частин рівності (5.3), дістанемо
 (5.4)
(5.4)
Замінимо в шуканому інтегралі (5.2) змінну інтегрування х і її диференціал dx їх значеннями (5.3) і (5.4). Цим ми приведемо інтеграл (5.2) до вигляду  , де
, де  є неперервною функцією аргументу t.
є неперервною функцією аргументу t.
Доведемо, що
 (5.5)
(5.5)
Для цього покажемо співпадання диференціалів лівої і правої частин рівності (5.5), якщо  або, що те саме,
або, що те саме,  . Маємо
. Маємо

Рівність (5.5) доведена.
Рівність (5.5) називають робочою формулою для обчислення інтегралів методом підстановки (методом заміни змінної).
Часто підінтегральний вираз  в обчислюваному інтегралі (5.2) можна записати у вигляді
в обчислюваному інтегралі (5.2) можна записати у вигляді
 .
.
В цьому випадку введемо позначення
 (5.6)
(5.6)
Дістанемо
 (5.7)
(5.7)
Подамо послідовність обчислення невизначених інтегралів методом підстановки.
10. Ввести нову змінну інтегрування за формулою (5.3) або (5.6).
20. Знайти диференціал від обох частин рівності (5.3) або (5.6).
30. Перейти до рівності (5.5) або (5.7).
40. Обчислити інтеграл у правій частині рівності (5.5) або (5.7).
50. В отриманому так результаті перейти до вихідної змінної.
Приклад.
Обчислити інтеграл
 .
.
Розв’язання.
1. Покладемо 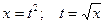 .
.
2. 
3.  .
.
4. 

5.  .
.
Приклад.
Обчислити інтеграл
 .
.
Розв’язання.
1. Покладемо 
2. 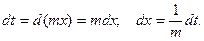 .
.
3.  .
.
4.  .
.
5. 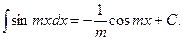 .
.
Аналогічними обчисленнями дістанемо таку таблицю (для сталих m і n):
1. 
2. 
3. 
4. 
5.  .
.
6.  .
.
7. 
8. 
9. 
10. 
11.Якщо  , то
, то
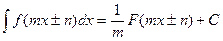
Приклад
Обчислити інтеграл

Розв’язання.
1. Покладемо 
2. 
3. 
4.  .
.
5.  .
.
Приклад.
Обчислити інтеграл

Розв’язання.
1. Покладемо 
2. 
3. 
4.  .
.
5.  .
.
Приклад
Обчислити інтеграл

Розв’язання.
1. Покладемо 
2. 
3. 
4.  .
.
5.  .
.
Приклад
Обчислити інтеграл

Розв’язання.
1. Покладемо 
2. 
3. 
4.  .
.
5.  .
.
Вправи
Обчислити інтеграли
1. 
(Відп. 
2. 
(Відп. 
3. 
(Відп. 
4. 
(Відп. 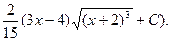
5. 
(Відп. 
6. 
(Відп. 
7. 
(Відп. 
8. 
(Відп. 
9. 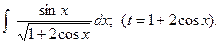
(Відп. 
10. 
(Відп. 
11. 
(Відп. 
12. 
(Відп. 
13. 
(Відп. 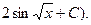
14. 
(Відп. 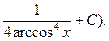
§5.5. Інтегрування частинами
Нехай функції  визначені й диференційовні на деякому проміжку
визначені й диференційовні на деякому проміжку  . За формулою диференціювання добутку, маємо
. За формулою диференціювання добутку, маємо

Візьмемо від обох частин цієї рівності невизначений інтеграл:
 .
.
Враховуючи, що  , дістанемо формулу:
, дістанемо формулу:
 (5.9)
(5.9)
Формулу (5.9) називають формулою інтегрування частинами, а інтегрування з її використанням – інтегрування частинами.
Для застосування формули (5.9) підінтегральний вираз розбивається на два множники: деякий аналітичний вираз, який входить до функції  , позначаємо через
, позначаємо через 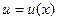 і його диференціюємо (обчислюємо
і його диференціюємо (обчислюємо 
 ); решту підінтегрального виразу позначаємо через
); решту підінтегрального виразу позначаємо через  і його інтегруємо (знаходимо v
і його інтегруємо (знаходимо v  ).Після чого до інтеграла
).Після чого до інтеграла  застосовуємо формулу (5.9). Тут ми допускаємо, що відшукання функції v(x) і обчислення інтеграла
застосовуємо формулу (5.9). Тут ми допускаємо, що відшукання функції v(x) і обчислення інтеграла  буде в сукупності простішою задачею, ніж обчислення інтеграла
буде в сукупності простішою задачею, ніж обчислення інтеграла  .
.
При користуванні формулою (5.9) не можна u i dv вибирати довільно, інакше можна одержати складніший інтеграл, ніж вихідний. Ми вкажемо окремі класи функцій, невизначені інтеграли від яких обчислюються інтегруванням частинами і дамо рекомендації з вибору u і dv. Ці функції можна розбити на три групи.
1.До першої групи належать функції, які мають множником функції: ln x, arcsin x, arccos x, arctg x, ln(j (x)),…. Саме ці функції треба позначати через u (x).
Приклад.
Обчислити інтеграл
 .
.
Розв’язання. Введемо позначення

Звідси

Тоді

Приклад
Обчислити інтеграл

Розв’язання. Введемо позначення

Звідси

Тоді

Невизначений інтеграл

інтегруємо методом підстановки.
1. Покладемо 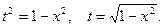
2. 
3. 
4. 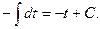
5. 
Остаточно знаходимо

II. До другої групи належать функції

де a, b, c – постійні; n – натуральне число. Тут формулою (5.9) треба користуватись n раз, при цьому кожен раз
 ,
,
де k почергово приймає значення n, n -1, …, 1.
Приклад
Обчислити інтеграл

Розв’язання. Введемо позначення

Звідси

Тоді

Невизначений інтеграл  будемо також інтегрувати частинами. Нехай
будемо також інтегрувати частинами. Нехай

Звідси

Отже

Остаточно знаходимо

III. До третьої групи належать функції

Двократним інтегруванням частинами дістаємо рівняння першого порядку відносно шуканого інтеграла.
Приклад.
Обчислити інтеграл

Розв’язання. Введемо позначення

Звідси

Тоді

Невизначений інтеграл  також інтегруємо частинами. Позначимо в цьому інтегралі
також інтегруємо частинами. Позначимо в цьому інтегралі

Звідси

Тоді

Отже
 .
.
У правій частині цієї рівності маємо той самий інтеграл, що й у лівій. Розв’язуючи цю рівність відносно інтеграла, знаходимо

Зауважимо, що вказані три групи не вичерпують всіх без винятку інтегралів, які беруться частинами.
Вправи
Обчислити інтеграли
1. 
(Відп. 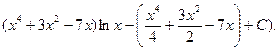
2. 

3. 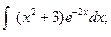

Дата публикования: 2014-11-19; Прочитано: 817 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
