Преобразования плоскости в себя

В первую очередь рассмотрим вопрос о существовании таких точек при аффинном преобразовании плоскости в себя (3.2), при котором эти точки переходили бы в себя, т.е. не меняли бы своего положения на плоскости. Такие точки называются неподвижными или двойными или инвариантными.

Естественно полагать, что для неподвижной точки должно соблюдаться условие: , .

Тогда, в выражение (3.2), запишем как

(3.8)

Решая систему уравнений (3.8) относительно переменных и , можно найти искомые координаты неподвижной точки:

, (3.9)

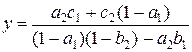. (3.10)

Однако, при решение системы уравнений (3.8) при конкретных значениях коэффициентов, могут иметь место три случая:

– система имеет одно решение;

– может не иметь ни одного решения;

– имеет бесчисленное множество решений.

В первом случае получаем одну неподвижную точку, во втором – отсутствие двойных точек, в третьем – прямолинейный ряд двойных точек, который принадлежит прямой линии, т.е. образуется двойная прямая (прямая неподвижных точек).

В последнем случае наблюдается пропорциональность коэффициентов:

.

Это обозначает, что оба уравнения (3.8) представляют собой одну и ту же прямую, все точки которой являются неподвижными. Этой прямой является ось перспективно-аффинного соответствия (см. п. 2.1.2).