Аналитическое представление аффинных преобразований

Пусть в плоскости имеем аффинную систему координат и задано геометрическое преобразование, переводящее произвольную точку 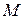в точку 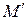. Тогда координаты и точки 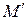однозначно определяются координатами и точки 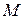, т.е. являются функциями от и :

, (3.1)

Теорема: геометрическое преобразование (3.1) плоскости тогда и только тогда является аффинным преобразованием, когда аффинные координаты и , преобразованной точки 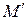являются линейными функциями координат и исходной точки :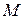

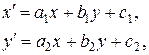(3.2)

причем, , т.е.

.

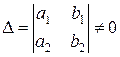Доказательство: покажем, что каждое преобразование (3.2) является аффинным.

Из уравнения (3.2) определим координаты и исходной точки :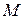

, (3.3)

. (3.4)

Выражения (3.3 и (3.4) можно получить следующим образом:

– запишем нижнее уравнение (3.2) в виде

,

которое подставим в верхнее уравнение (3.2) и получим

,

– аналогично для определения из нижнего уравнения (3.2) сначала имеем

,

а, подставляя последнее в верхнее уравнение (3.2), получаем

.

Полученные зависимости показывают линейность и от и :

(3.5)

где

, , ;

, , .

Попутно отметим, что преобразование (3.2) переводит точки , , , соответственно в точки , , , имеющие координаты: , ; , ; , .

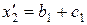Тогда точки, координаты которых удовлетворяют уравнению первой степени (прямой линии)

(3.6)

перейдут в точки, координаты которых удовлетворяют уравнению

, (3.7)

где , , .

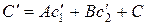Таким образом, преобразование (3.2) переводит любую прямую (3.6) плоскости снова в прямую, т.е. является аффинным.