Аффинные координаты

Декартова (прямоугольная) система осей координат не может быть применена в аффинной геометрии. Однако, если ее подвергнуть произвольному аффинному преобразованию, то можно заменить ее аффинной конструкцией.

На рисунке 3.1 показано задание декартовой системы осей координат и положение точки 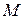относительно данной системы.

Рисунок 3.1– Задание декартовой системы осей координат

Таким образом, имеем точку , для которой

, ,

где

,

;

, т.е. ,

, т.е. ;

Здесь 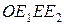– единичный квадрат.

Произведем аффинное преобразование плоскости вместе с находящейся на ней системой (рисунок 3.2).

Рисунок 3.2– Аффинное преобразование координатной плоскости

На этом рисунке – единичный параллелограмм,

,

;

,

.

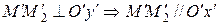Прямым и соответствуют прямые 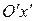и , пересекающиеся под произвольным углом, а прямым и – прямые и . Координаты точки 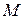не будут равны расстояниям точки 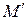от прямых и 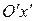, но они будут равны отношениям соответствующих отрезков. Таким образом, получена точка , для которой координаты

и ,

являются аффинными координатами.

По характеристическому свойству аффинных преобразований (сохранение коллинеарности и простого отношения трех точек прямой) координаты точки 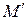остаются равными ; .

Поэтому, чтобы иметь возможность однозначно находить координаты для любой точки плоскости, достаточно знать положение трех ее точек – , которые в силу теории аффинных преобразований могут быть произвольными, но не лежащие на одной прямой.

Таким образом, с помощью аффинного преобразования декартовой системы получена новая обобщенная аффинная система координат, которая представляет обобщение декартовой, так как в ней масштабы 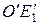и по осям различны. Кроме того, единичный квадрат 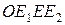декартовой системы заменился единичным параллелограммом , т. е. декартова система координат представляет собой тот частный случай аффинной системы, когда масштабы по осям равны.

Всякое новое аффинное преобразование плоскости переводит аффинную систему координат в аффинную же.

Способ задания аффинной системы координат представлен рисунком 3.3, на котором показаны:

– координатный репер 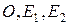, как три произвольные точки, не лежащие на одной прямой;

– начало координат, точка ;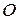

– оси координат и .

Таким образом, имеем оси координат вместе с заданными на них единичными точкам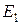и и , т.е. аффинную систему координат.

Рисунок 3.3– Способ задания аффинной системы координат

Аффинным координатам точки ставятся в соответствие два числа:

и .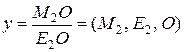

Итак, если имеем какую-то аффинную систему координат и выполняем аффинное преобразование, переводящее данную систему в новую аффинную систему координат, то координаты каждой точки в первоначальной системе совпадут с координатами образа этой точки в преобразованной системе. Отсюда следует, что уравнение любой линии в исходной системе координат совпадает с уравнением образа этой линии в преобразованной системе. Вообще всякая аналитическая формула, выражающая какое-нибудь аффинное свойство фигуры в прямоугольных декартовых координатах, будет выражать это же свойство и в обобщенной аффинной системе координат.

Еще один важный аспект: все системы аффинных координат эквивалентны между собой, т.е. в вопросах аффинной геометрии все аффинные системы координат являются равноправными.