Полюс — плоскость по координате z

Для плоскопараллельного поля суммарный поток с правой половины торца полюса и грани в (рис.) можно опреде­лить как

(2.4)

Здесь FT— магнитное напряжение между торцевыми поверхностя­ми полюсов; Fzb— то же между точками А' и В' (рис. 4.16, д); GТ— полная проводимость воздушного зазора между тор­цевой поверхностью правой половины полюса и плоско­стью.

Тогда

. (2.5)

Необходимо отметить, что в случае плоскопараллельного поля удельная проводимость ребра торца от ширины полюса не зависит, а для граней а и в они равны. Магнитная проводимость между пра­вой и боковой гранью и плоскостью

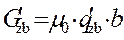, (2.6)

где q’zb— удельная проводимость между правой боковой гранью в и плоскостью, полученная для плоскопараллельного поля. Чтобы сложное поле между полюсом и плоскостью с максимальной индук­цией В_т в зазоре б заменить эквивалентным однород­ным полем, необходимо увеличить размер полюса а. Обозначая расчетный размер правой половины полюса через а_р, получим суммарный поток с торца и боковой грани в

(2.7)

Приравняв уравнения (2.4) и (2.7) для правой половины полюса, будем иметь

(2.8)

Аналогично для левой половины полюса

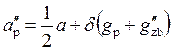(2.9)

Полный расчетный размер для грани а

(2.10)

Аналогично определяются расчетные размеры для грани в:

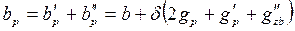(2.11)

Тогда полная расчетная проводимость воздушного зазора для эквивалентного однородного поля, которое учитывает поле выпу­чивания, представится

(2.12)

Таким образом, проводимость воздушного зазора с учетом поля выпучивания определяется довольно просто. Расчет значительно облегчается, если удельные проводимости с боковых граней опре­делять из кривых, построенных по формулам ряда авто­ров. При определении удельной боковой проводимости авто­ры исходили из разных условий вывода формул. Это привело к тому, что величина удельной проводимости поля с ребра торца получилась различной, поэтому для случая полюс — плоскость по Ротерсу следует брать =0,52.

РАСЧЕТ МАГНИТНЫХ ПРОВОДИМОСТЕЙ