Коллигативные свойства растворов электролитов. Изотонический коэффициент Вант-Гоффа

Законы Вант-Гоффа и Рауля справедливы для идеальных растворов, т.е. таких, в которых нет химического взаимодействия между компонентами раствора, а также не происходит диссоциация или ассоциация частиц растворенного вещества. Для данных систем экспериментально найденные и теоретически рассчитанные величины р_осм., Dt_кип., Dt_зам., 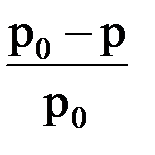совпадают.

Реальные растворы электролитов по своим свойствам отличаются от идеальных.

Так, для растворов электролитов экспериментально найденные значения вышеперечисленных величин всегда больше, чем рассчитанные по законам Вант-Гоффа и Рауля. Т.е., растворы электролитов на практике ведут себя так, как будто они содержат больше частиц растворенного вещества, чем это следует из их аналитической концентрации. Исходя из этого, Вант-Гофф предложил для растворов электролитов при теоретическом расчете р_осм., Dt_кип., Dt_зам., использовать поправочный коэффициент i, который получил название коэффициента Вант-Гоффа или изотонического коэффициента:

р_осм. = iCRT; Dt_кип. = iEm; Dt_зам. = iKm; 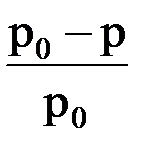= ic₁.

Изотонический коэффициент показывает, во сколько раз реальное число частиц растворенного вещества больше, чем теоретически ожидаемое (если предполагать, что вещество в растворе присутствует только в виде молекул).

Для идеальных растворов электролитов i >1.

Коэффициент Вант-Гоффа показывает также, во сколько раз наблюдаемое опытное значение р_осм., Dt_кип., Dt_зам., больше теоретически вычисленного, т.е.:

Причину отклонения растворов электролитов от законов Рауля и Вант-Гоффа впервые объяснил шведский ученый С. Аррениус. Он показал, что электролиты за счет действия молекул растворителя распадаются на ионы. Этот процесс приводит к увеличению реального числа частиц растворенного вещества.

Максимально значение изотонического коэффициента (i_max) для любого электролита будет при этом равно числу ионов, которые образуются при полной диссоциации его молекулы (или формульной единицы), т.к. именно во столько раз возрастет число частиц электролита в растворе.

Сванте Аррениус (1859 – 1927). Шведский физикохимик, основные работы которого посвящены учению о растворах и кинетике химических реакций. Он получил Нобелевскую премию по химии в 1903 году за создание теории электролитической диссоциации. Также им была разработана одна из наиболее известных теорий кислот и оснований. Однако еще большую известность имеют его работы в области химической кинетики. С. Аррениус высказал мысль, что реакционными являются не все, а только активные молекулы. Он ввел понятие энергии активации и вывел уравнение зависимости константы скорости реакции от температуры, носящее его имя.

Так, для NaCl i_max = 2, для Na₃PO₄ i_max = 4.

В реальных растворах диссоциация часто протекает не полностью, особенно если электролит является слабым.

Кроме того, наблюдаются межионные взаимодействия, приводящие к уменьшению числа кинетически активных частиц.

В этом случае величина i будет меньше его возможного максимального значения и будет зависеть от степени диссоциации электролита:

i = 1 + α (m – 1)

где α – степень диссоциации электролита (в долях единицы); m – число ионов, образующихся при полном распаде одной молекулы или одной формульной единицы электролита.

Таким образом, из двух растворов однотипных электролитов (т.е. распадающихся на одно и то же число ионов) с одинаковой молярной концентрацией изотонический коэффициент будет больше в растворе электролита с более высокой степенью диссоциации α. Соответственно, и р_осм., Dt_кип., Dt_зам. для такого раствора тоже будут иметь большие значения.

Если же молярная концентрация и степень диссоциации электролитов разного типа в растворе одинаковые, то значение i будет выше для электролита, диссоциирующего на большее число ионов m.