Постоянном магнитном поле

Выражение для силы Лоренца позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца и направление вызываемого ею отклонения заряженной частицы в магнитном поле зависят от знака заряда частицы. На этом основано определение знака заряда частиц, движущихся в магнитных полях.

Для вывода общих закономерностей будем считать, что магнитное поле однороднои на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В равен 0 или p. Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью v, перпендикулярной вектору В, то сила Лоренца F = q[vB] постоянна по модулю и нормальна к траектории частицы (рис.2.4). Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Отсюда следует, что частица будет двигаться по окружности, радиус Rкоторой определяется из условия QvB = mv²/R, откуда .

Период вращения частицы, т. е. время Т, за которое она совершает один полный оборот,

т. е. период вращения частицы в однородном магнитном поле определяется только величиной, обратной удельному заряду (q/m) частицы, и магнитной индукцией поля, но не зависит от ее скорости (при v ≪ c ). На этом основано действие циклических ускорителей заряженных частиц.

Если скорость v заряженной частицы направлена под углом a к вектору В (рис.2.5), то ее движение можно представить в виде суперпозиции:

1) равномерного прямолинейного движения вдоль поля со скоростью

v₁ = vcosa; 2) равномерного движения со скоростью v_^ = vsina по окружности в плоскости, перпендикулярной полю. Радиус окружности

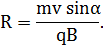
В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю (рис.2.5).

Шаг винтовой линии

Рисунок 2.5 - Общий случай движения заряженной частицы в магнитном поле

Подставив в выражение формулу для периода, получим

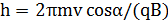
Направление, в котором закручивается спираль, зависит от знака заряда частицы. Если скорость v заряженной частицы составляет угол a с направлением вектора В неоднородного магнитного поля, индукция которого возрастает в направлении движения частицы, то R и h уменьшаются с ростом В. На этом основана фокусировка заряженных частиц в магнитном поле.