Магнитные поля соленоида и тороида

Рассчитаем, применяя теорему о циркуляции, индукцию магнитного поля внутри соленоида. Рассмотрим соленоид длиной l, имеющий N витков, по которому течет ток. Длину соленоида считаем во много раз больше, чем диаметр его витков, т. е. рассматриваемый соленоид бесконечно длинный. Экспериментальное изучение магнитного поля соленоидапоказывает, что внутри соленоида поле является однородным, вне соленоида — неоднородным и очень слабым.

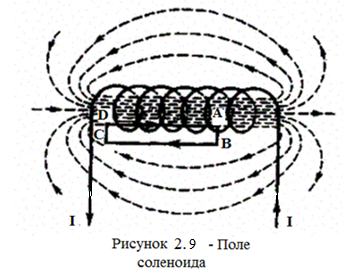На рис. 2.9 представлены линии магнитной индукции внутри и вне соленоида. Чем соленоид длиннее, тем меньше магнитная индукция вне его. Поэтому приближенно можно считать, что поле бесконечно длинного соленоида сосредоточено целиком внутри него, а полем вне соленоида можно пренебречь.

Для нахождения магнитной индукции В выберем замкнутый прямоугольный контур ABCDA, как показано на рис. 2.9. Циркуляция вектора В по замкнутому контуру ABCDA, охватывающему все N витков, согласно теореме о циркуляции, равна

Интеграл по ABCDA можно представить в виде четырех интегралов: по АВ, ВС, CD и DA. На участках АВ и CDконтур перпендикулярен линиям магнитной индукции и В=0. На участке вне соленоида В=0.На участке DAциркуляция вектора В равна В1(контур совпадает с линией магнитной индукции); следовательно,

Отсюда приходим к выражению для магнитной индукции поля внутри соленоида (в вакууме):

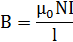
Получили, что поле внутри соленоида однородно ( краевыми эффектами в областях, прилегающих к торцам соленоида, при расчетах пренебрегают). Однако отметим, что вывод этой формулы не совсем корректен (линии магнитной индукции замкнуты, и интеграл по внешнему участку магнитного поля строго нулю не равен). Корректно рассчитать поле внутри соленоида можно, применяя закон Био — Савара — Лапласа; в результате получается та же формула.

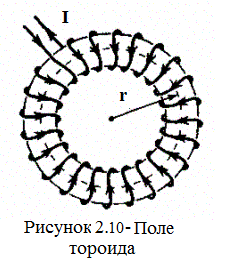Важное значение для практики имеет также магнитное поле тороида — кольцевой катушки, витки которой намотаны на сердечник, имеющий форму тора (рис. 2.10). Магнитное поле, как показывает опыт, сосредоточено внутри тороида, вне его поле отсутствует.

Линии магнитной индукции в данном случае, как следует из соображений симметрии, есть окружности, центры которых расположены по оси тороида. В качестве контура выберем одну такую окружность радиуса r. Тогда, по теореме о циркуляции, B×2pr = m₀NI, откуда следует, что магнитная индукция внутри тороида (в вакууме)

,

где N— число витков тороида.

Если контур проходит вне тороида, то токов он не охватывает и B×2pr = 0. Это означает, что поле вне тороида отсутствует (что показывает и опыт).

Контрольные вопросы первого уровня

1. Как определяется сила Лоренца? Как определить направление силы Лоренца?

2. Чему равна работа силы Лоренца, действующей на заряженную частицу?

3. По какой траектории движется частица, если V^ B?

4. Чему равен радиус окружности, по которой движется заряженная частица?

5. Чему равен период движения частицы по окружности?

6. По какой траектории движется частица, если влетает в магнитное поле под углом к вектору магнитной индукции?

7. Как изменяется шаг и радиус спирали при уменьшении поля?

8. Что называется эффектом Холла? Какова причина эффекта Холла? Что можно сказать по постоянной Холла?

9. Что называется циркуляцией вектора магнитной индукции? Записать закон полного тока для магнитного поля в вакууме.

10. Магнитная индукция поля соленоида и тороида.

Методические указания по решению задач

Большинство задач данного раздела связано либо с равновесием, либо с движением тел под действием различных сил, включая силу Ампера и силу Лоренца. Поэтому, наряду с законами магнетизма, при решении задач необходимо использовать законы механики.

Цель: Решение задач, связанных с движением заряженных частиц в магнитном поле.