Уравнения и свойства многополюсников

При описании электрической цепи ее зачастую представляют как совокупность фрагментов более общего вида (чем четырех- и двухполюсники), имеющих произвольное число внешних зажимов (полюсов), через которые такой фрагмент — многополюсник — соединяется с другими участками цепи (рис. 8.14).

Рис. 8.14

Описание многополюсника как элемента цепи выражает связи между токами полюсов İk и напряжениями входных узлов Uk относительно опорного узла цепи 0. В общем виде такая связь для линейного многополюсника может быть выражена в матричной форме: İ = YU,

где , — векторы токов и напряжений полюсов;

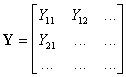— неопределенная матрица проводимостей многополюсника — квадратная матрица размера п.

Матрица Y называется неопределенной, поскольку ее элементы Y_jk не являются независимыми друг от друга, так как токи полюсов, образующих сечение цепи, связаны друг с другом первым законом Кирхгофа и, следовательно, отдельные уравнения системы являются линейно зависимыми. Поэтому неопределенная матрица проводимостей многополюсника является вырожденной — ее определитель равен нулю.

Например, описание двухполюсника с помощью неопределенной матрицы проводимостей Y (рис. 8.15) выражается двумя уравнениями:

или в матричной форме

Рис. 8.15

Отсюда видно, что всю существенную информацию о двухполюснике несет лишь один выделенный элемент неопределенной матрицы Y 11 = Y. Недиагональные элементы неопределенной матрицы проводимостей пассивного многополюсника Ymk с одинаковыми индексами на основании принципа взаимности равны друг другу: Ymk = Ykm.

Для трехполюсных элементов цепи — трехполюсников (рис. 8.16), к которым относятся, например, транзисторы, система уравнений для токов имеет вид:

Рис. 8.16

По первому закону Кирхгофа в этом случае имеем

Так как это равенство выполняется при любых значениях то суммы проводимостей Y_km в каждой скобке должны быть равны нулю. Поэтому сумма элементов каждого столбца неопределенной матрицы проводимостей любого многополюсника — это справедливо не только для трехполюсника — равна нулю.

С другой стороны, если все входы многополюсника находятся под одинаковым потенциалом то токи через все выходные зажимы не протекают — İ_k = 0. Поэтому и сумма элементов каждой строки неопределенной матрицы проводимостей многополюсника равна нулю.

Эти свойства позволяют записать неопределенную матрицу проводимостей трехполюсника в форме:

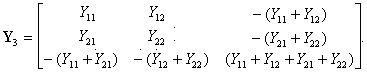
Таким образом, вся существенная информация о трехполюснике содержится лишь в выделенной клетке матрицы с элементами Y ₁₁, Y ₁₂, Y ₂₁, Y ₂₂. Эта клетка соответствует описанию трехполюсника как четырехполюсника, у которого зажим 3 является общим для входной и выходной пар полюсов. Такие четырехполюсники с общим зажимом являются весьма распространенными, и, следовательно, вся рассмотренная выше теория четырехполюсников распространяется и на трехполюсники с общим зажимом для входной и выходной цепей.

При анализе цепей с транзисторами часто бывает необходимо выразить параметры схемы с одним общим зажимом через параметры той же схемы с другим общим зажимом. Это осуществляют с помощью неопределенной матрицы проводимостей. Для записи матрицы проводимостей четырехполюсника с k -м общим зажимом входной и выходной цепей из неопределенной матрицы проводимостей трехполюсника Y₃ следует просто вычеркнуть k -ю строку и k -й столбец. Так, при общем зажиме 2 матрица проводимостей четырехполюсника с входными 12 и выходными 32 зажимами имеет вид:

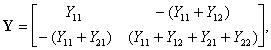
где Y ₁₁, Y ₁₂, Y ₂₁ и Y ₂₂ — элементы матрицы четырехполюсника с общим зажимом 3, входными 13 и выходными 23 зажимами.

8. 11. Определение параметров четырехполюсников
(задачи с решением)

Задача 8.1. Определить А -параметры четырехполюсника (см. п. 8.1 теоретического материала), схема которого представлена на рис. П11.1. Рис. П11.1.

При холостом ходе на выходе четырехполюсника , и из общей системы уравнений четырехполюсника через А -параметры

найдем . Из анализа схемы непосредственно следует, что в этом режиме , откуда А ₁₁ = 1, а , т.е. А ₂₁ = 1/ Z ₁.

Аналогично, при коротком замыкании на выходе четырехполюсника , и из системы имеем . Теперь анализ схемы дает , следовательно, А ₁₂ = Z ₂, а А ₂₂ = 1+ Z ₂/ Z ₁.

Запишем результат в матричной форме

.

Нетрудно убедиться, что найденные параметры удовлетворяют соотношению А ₁₁ А ₂₂  А ₁₂ А ₂₁ = 1, справедливому для обратимых четырехполюсников.

Задача 8.2.Определить Z -параметры составного четырехполюсника (рис. П11.2, а), рассматривая их как последовательное, параллельное или каскадное соединение простейших одноэлементных четырехполюсников.

Перекрытый Т-образный четырехполюсник (рис. П11.2, а) может быть представлен в виде последовательного соединения П-образного четырехполюсника Z ' (Z ₁, Z ₃, Z ₁) и одноэлементного — Z ₂ (рис. П11.2, б).

a) б)

Рис. П11.2

Четырехполюсник Z ' — это каскадное соединение одноэлементных четырехполюсников — параллельного Z ₁, последовательного Z ₃ и параллельного Z ₁. A -матрицы этих четырехполюсников можно получить из результата предыдущей задачи, полагая в нем Z ₂ = 0 для параллельного четырехполюсника и Z ₁ = ∞ для последовательного и соответственно изменяя обозначения. Перемножение A -матриц дает:

Поскольку далее будет рассматриваться последовательное соединение, перейдем к Z -параметрам. Для этого воспользуемся связями между различными системами параметров.

Имеем:

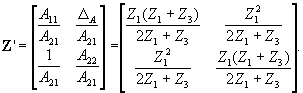
Z -параметры одноэлементного четырехполюсника Z ₂, описываемого матрицей (см. п. 8.3, рис.8.5, a)

,

можно получить тем же путем перехода от его А -параметров к Z -параметрам.

Z -параметры последовательно соединенных четырехполюсников суммируются Z = Z'+ Z". Поэтому окончательно получим для Z -параметров перекрытого Т-образного четырехполюсника:

Задача 8.3. Определить характеристические параметры четырехполюсника, рассмотренного в задаче 8.1, принимая в качестве элементов схемы Z 1 = 1/ jωC, Z 2 = jωL. Для характеристических сопротивлений справедливы следующие выражения через А -параметры (см. п. 8.7) . Подстановка полученных в задаче 11.1. выражений А -параметров с учетом характера элементов дает . Для меры передачи четырехполюсника имеем . Из полученных выражений следует, что при оба характеристических сопротивления вещественны, а мера передачи — чисто мнимая величина g = jβ. При , наоборот, характеристические сопротивления — мнимые, а мера передачи имеет ненулевую вещественную часть.
Задача 8.4. Рассчитать коэффициенты передачи по напряжению и току однородной цепной LC- схемы, рассмотренной в Примере п.8.9, состоящей из четырех звеньев, при соотношении между ее параметрами в режимах согласованной нагрузки, холостого хода и короткого замыкания.

При для характеристических параметров одного звена имеем (см. п. 8.9):

Поэтому в режиме согласования — при нагрузке цепной схемы на резистор с сопротивлением ее каждое звено дает фазовый сдвиг напряжения и тока на π /2, а их действующие значения остаются неизменными, поскольку коэффициент затухания α = 0. Четыре звена схемы дают фазовый сдвиг на 2 π,т.е. в режиме согласования входные и выходные токи и напряжения четырехзвенной схемы равны друг другу.

Для определения связей между токами и напряжениями при холостом ходе и коротком замыкании определим А- параметры схемы А ₁₁ и А ₂₂. Поскольку четырехполюсник симметричный, то оба эти параметра равны друг другу и выражаются как А ₁₁ = А ₂₂ = ch(4 g) = ch(4 j π /2) = cos(2 π) = 1. Поскольку эти параметры выражают отношение входного и выходного напряжений при холостом ходе и токов при коротком замыкании, то и эти отношения будут равны единице — при холостом ходе входное и выходное напряжения четырехзвенной схемы равны друг другу, также как и токи при коротком замыкании.