Краткие теоретические сведения. Четырёхполюсник обладает свойствами фильтра только в том случае, когда

Четырёхполюсник обладает свойствами фильтра только в том случае, когда

сопротивления Z₁ = ± j X₁ и Z₂ = ± j X₂, входящие в Г - образные или

симметричные Т - и П - образные схемы (рис.47,48), имеют разные знаки.

Электрический фильтр наилучшим образом выполняет свои функции, если

он нагружен на сопротивление, равное характеристическому сопротивлению.

В теории фильтров, основанной на характеристических параметрах

четырёхполюсников, решаются следующие основные задачи:

1) устанавливаются условия, при которых фильтр имеет полосу

прозрачности;

2) определяется ширина полосы прозрачности;

3) находятся уравнения частотных характеристик (АЧХ и ФЧХ).

Для Г - образного звена - прототипа (рис.47) справедлива система

уравнений в параметрах прямой передачи:

Рис.47

Определим А - параметры из режимов холостого хода и короткого

замыкания на выходе:

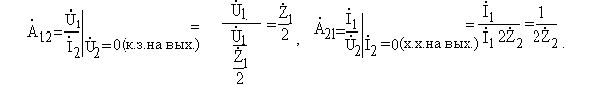
В теории четырёхполюсников показано, что характеристические

сопротивления (входные сопротивления в режиме двустороннего

согласования) определяются

Постоянная передачи (мера передачи) g = a + jb может быть определена

из соотношения:

Т - и П - образные симметричные четырёхполюсники получаются

каскадным согласованным соединением двух Г-образных четырехполюсников

(рис.48), поэтому их постоянные передачи равны удвоенному значению

постоянной передачи Г- образного звена-прототипа.

Рис.48

Для Т - и П - образных симметричных схем

Характеристические сопротивления полученных звеньев остаются равными

соответствующим сопротивлениям Г - образного звена.

Так как фильтр нагружен на сопротивление, равное характеристическому,

соотношение напряжений и токов его на входе и выходе

Из определения полосы прозрачности следует, что затухание а = 0;

фазовая же постоянная b в этой полосе частот может быть отличной от нуля.

Поэтому в полосе прозрачности g = a + jb оказывается мнимой величиной

и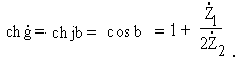

Поскольку cos b не может быть больше единицы, то необходимым условием

наличия полосы прозрачности является разный характер сопротивлений Z₁ и

Z₂, т. е. если Z₁ = j X₁ положительно (имеет индуктивный характер), то Z₂

= - j X₂ должно быть отрицательным (ёмкостным) и наоборот. Это условие

необходимо, но не является достаточным.

cos b может изменяться в пределах от - 1 до + 1, следовательно

Таким образом, для существования полосы пропускания необходимо и

достаточно, чтобы сопротивления X₁ и X₂ имели разные знаки, а по

абсолютной величине X₁ было бы меньше 4X₂: |X₁| < 4 |X₂|.

Граничные частоты полосы пропускания (частоты среза) можно определить

несколькими способами, используя основное неравенство теории фильтров

1. Если задан вид функций Z₁() и Z₂(), то граничные частоты

находятся из решения системы уравнений

2. Если частотные зависимости Z₁() и Z₂() заданы графически, то

граничные частоты полосы пропускания могут быть также определены

графически (рис.49).

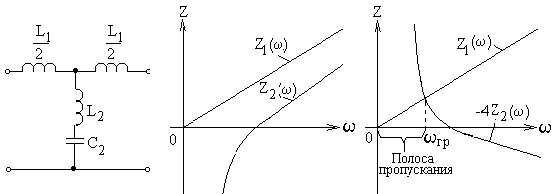
Рис.49

3. Граничные частоты могут быть найдены из рассмотрения зависимости

входного сопротивления фильтра, согласованного на выходе, т.е. с помощью

характеристического сопротивления:

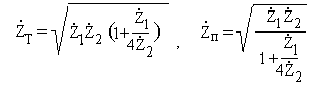
При разных знаках Z₁() и Z₂(), а также при

произведение Z₁() на Z₂() действительное положительное число,

следовательно, характеристические сопротивления в полосе пропускания

являются действительными.

Поскольку характеристическое сопротивление четырёхполюсника является

средним геометрическим входных сопротивлений в режиме холостого хода - Z_x и

короткого замыкания - Z_к, то граничные частоты могут быть определены как

частоты, в пределах которых Z_x и Z_к имеют разные знаки (рис.50).

Рис.50

4. Выше было показано, что

где

комплексный коэффициент передачи по напряжению в режиме холостого хода

на выходе.

В полосе пропускания

Из последнего выражения для модуля коэффициента передачи получим

Для граничных частот это неравенство обращается в равенство:

Таким образом, граничные частоты могут быть определены как частоты, на

которых коэффициент передачи при холостом ходе равен единице. Это

определение особенно удобно при экспериментальном исследовании фильтров.

Частотными характеристиками фильтра являются зависимости:

а() амплитудно-частотная характеристика,

b() фазо-частотная характеристика.

Для нахождения уравнений частотных характеристик используем выражение

для постоянной передачи Г - образного звена

Разделив вещественную и мнимую части, получим

В полосе пропускания а = 0 следовательно , и

Поскольку сопротивления Х₁ и Х₂ зависят от частоты, то из

последнего уравнения получим зависимость коэффициента фазы от частоты в

полосе пропускания (ФЧХ) в виде

Амплитудно-частотная характеристика в полосе пропускания а() = 0

сливается с осью частот.

В полосе подавления следовательно,

отсюда b=± и а значит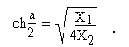

Уравнение амплитудно-частотной характеристики в полосе подавления

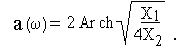
Фазо-частотная характеристика в полосе подавления b()=±

Пример 1. Для схемы П- образного ФНЧ (рис.51), согласованного с

нагрузкой, рассчитать токи во всех ветвях и напряжения на элементах при

заданном входном напряжении. Построить векторные диаграммы рассчитанных

токов и напряжений.

Рис.51

Решение. Для П - образного фильтра нижних частот

,

значит фильтр работает в полосе пропускания и затухание а = 0.

Характеристическое сопротивление

Коэффициент фазы

Рассчитаем граничную частоту фильтра

(Заданная по условию частота находится в полосе пропускания фильтра).

Выходное напряжение

Напряжение на индуктивности

Токи в ветвях

Рис.52

Векторная диаграмма токов и напряжений, построенная по результатам

расчетов, приведена на рис.52.

Пример 2. Изменим в предыдущем примере частоту так, чтобы получить

полосу подавления, например = 4000 р/c.

Тогда

значит фильтр работает в полосе подавления и

Характеристическое сопротивление

Затухание

Выходное напряжение

Напряжение на индуктивности

Токи в ветвях

Рис.53

Векторная диаграмма токов и напряжений в полосе подавления приведена

на рис.53.