Векторное произведение двух векторов

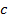Векторным произведением двух называется вектор , длина которого равна площади параллелограмма, построенного на векторах 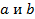, перпендикулярный к плоскости этих векторов и направленный так, чтобы кратчайший поворот от 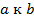вокруг полученного вектора 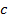представлялся происходящим против часовой стрелки, если смотреть из конца вектора 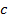(рис.3.13).

b

a

с

Рис.3.13. Векторное произведение

O

r

A

P

F

Рис.3.14. Момент силы

Из этого определения следует, что длина вектора 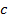равна:

. (3.12)

Векторное произведение Векторное произведение равно нулевому вектору в том и только в том случае, когда по крайней мере один из перемножаемых векторов является нулевым или когда эти векторы параллельны, т.е. если векторы коллинеарны.

Таким образом, условием коллинеарности векторов будет:

. (3.13)

В частности, всегда .

Замечание 3.2. Условие (3.13) коллинеарности двух векторов можно заменить следующим: , где 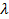-некоторое число (считая ).

Если векторы a и b взаимно перпендикулярны, то sin()=1, и, значит, длина вектора-произведения равна произведению длин векторов сомножителей, т.е. в этом случае

Пример 3.10. Проверить справедливость равенства .

Векторы направлены по осям координат Ox и Oy, тогда вектор 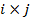будет направлен по оси Oz. С другой стороны, его длина равна площади прямоугольника, построенного на векторах , т.е. 1. Следовательно, .

Отметим, что аналогично доказывается, что

.

Пример 3.11. Показать, что

Действительно,

складывая эти два равенства, находим:

.

В механике важное значение имеет понятие момента относительно данной точки. Если сила 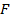приложена к точке A (рис. 3.14), то моментом силы 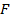относительно точки O называется вектор , определяемый формулой

,

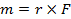где есть радиус-вектор точки приложения. Из определения векторного произведения следует, что величина момента равна величине силы, умноженной на расстояние OP точки O от прямой, вдоль которой действует сила (расстоянием от точки до прямой называется длина перпендикуляра, опущенного из точки на прямую).

Свойства векторного произведения.

1. При перестановке сомножителей векторное произведение умножается на (-1), т.е. .

В самом деле, площадь параллелограмма, построенного на векторах 2 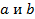, не меняется при перестановке 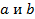. Поэтому векторы и имеют одинаковые длины и коллинеарны. Их же направления противоположны.

2. 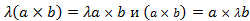, т.е. чтобы умножить векторное произведение векторов на число, достаточно умножить на это число один из сомножителей.

3.Векторное произведение подчиняется распределительному (дистрибутивному) закону, т.е. .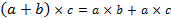

Для доказательства заметим сначала, что произведение a , где - единичный вектор (), можно построить так (рис.3.15а). Спроектируем вектор 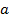на плоскость, перпендикулярную к 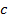, и полученную вектор-проекцию , повернем в этой плоскости вокруг точки 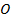по часовой стрелке на (если смотреть на плоскость с конца вектора ).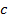

Полученный вектор и равен В самом деле,

,

где 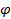-угол между векторами ; вектор перпендикулярен к векторам 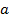и 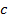и направлен в ту сторону, из которой кратчайший поворот от 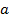к 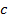представляется совершающимся против часовой стрелки. Итак, .

Пусть теперь даны единичный вектор 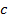, перпендикулярная к нему плоскость 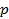и треугольник (рис.3.16б), в котором

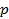Спроектируем треугольник на плоскость и повернем эту проекцию в плоскости 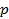по часовой стрелке на .

Получим треугольник , в котором по ранее доказанному

.

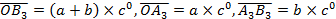Так как , то

(3.14)

Заметив, что умножим теперь обе части равенства (3.14) на скаляр 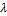. Применив свойство 2 векторного произведения, получим:

или () , что и требовалось доказать.

а) б)

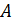
a

p

b

a

a+b

Рис.3.15. Распределительный закон для векторного произведения

Пример 3.12. Показать, что , и выяснить геометрический смысл этого равенства. В самом деле:

.

Это равенство означает, что удвоенная площадь параллелограмма, построенного на векторах 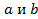равна площади параллелограмма, построенного на его диагоналях.

4. Рассмотрим, как векторное произведение векторов

и выражается через их координаты:

Так как

пример 3.10), то

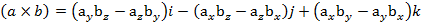. (3.15)

Формулу (3.15) легко запомнить, если воспользоваться определителем третьего порядка. Если формальную конструкцию

расписать по правилам вычисления определителя третьего порядка, то получится правая часть равенства (3.15), поэтому имеет место следующее формальное равенство: