 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Обратная матрица. Ранее мы видели, что найти решение системы можно, используя обратную матрицу
|
|
Ранее мы видели, что найти решение системы можно, используя обратную матрицу. Обратные матрицы нужны так же и при решении матричных уравнений, имеющих вид:
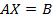 ,
,
где 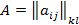 ,
,  ,
, 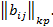
Изложим два способа вычисления обратной матрицы: первый из них даст ответ на вопрос о существовании обратной матрицы, второй является более эффективным с точки зрения вычислений.
Рассмотрим квадратную матрицу 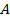 , имеющую порядок
, имеющую порядок 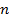
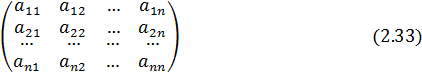
Союзной по отношению к матрице 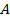 называется матрица
называется матрица 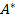 , которая строится следующим образом: сначала каждый элемент матрицы
, которая строится следующим образом: сначала каждый элемент матрицы 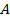 заменяется его алгебраическим дополнением, а затем полученная матрица транспонируется.
заменяется его алгебраическим дополнением, а затем полученная матрица транспонируется.
Теорема 2.3. Квадратная матрица 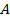 тогда и только тогда имеет обратную, когда ее определитель не равен нулю (
тогда и только тогда имеет обратную, когда ее определитель не равен нулю ( ), при этом
), при этом
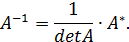
Доказательство. Проведем его на примере матрицы третьего порядка. Покажем, что
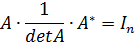
.
Имеем:

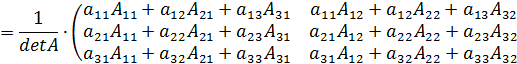

Элементы последней матрицы, не лежащие на главной диагонали, являются суммами произведений элементов какой-то строки матрицы 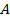 на алгебраические дополнения элементов какой-то другой ее строки. Ранее было показано, что такие суммы равны нулю. Диагональные же элементы являются разложением определителя матрицы
на алгебраические дополнения элементов какой-то другой ее строки. Ранее было показано, что такие суммы равны нулю. Диагональные же элементы являются разложением определителя матрицы 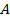 по элементам соответствующей строки, а потому они равны определителю матрицы
по элементам соответствующей строки, а потому они равны определителю матрицы 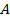 . Деля эту матрицу на
. Деля эту матрицу на 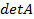 (а делить можно тогда и только тогда, когда
(а делить можно тогда и только тогда, когда  ) получим единичную матрицу. Так как союзная матрица отличается от обратной только множителем, то из существования обратной матрицы следует и существование союзной и, следовательно, в этом случае
) получим единичную матрицу. Так как союзная матрица отличается от обратной только множителем, то из существования обратной матрицы следует и существование союзной и, следовательно, в этом случае 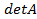
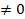 . Теорема доказана.
. Теорема доказана.
Пример 2.11. Найти матрицу, обратную к матрице 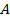 , если
, если
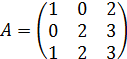 .
.
Решение. 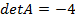 , следовательно обратная матрица существует. Вычислим алгебраические дополнения:
, следовательно обратная матрица существует. Вычислим алгебраические дополнения:

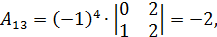
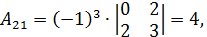
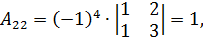
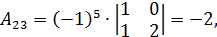

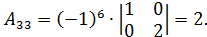
Тогда союзной будет матрица
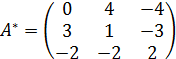 ,
,
а обратной – матрица
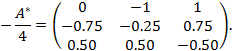
Для проверки правильности вычислений можно полученную матрицу умножить на исходную. Мы оставляем это читателю.
Рассмотрим другой метод вычисления обратной матрицы, использующий преобразования, применявшиеся нами при вычислении определителей и при решении систем линейных уравнений. Итак, вычислим обратную матрицу, используя схему метода Гаусса.
Для вычисления матрицы, обратной матрице (2.33), рассмотрим матрицу 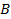 , состоящую из двух частей, одна из которых это матрица
, состоящую из двух частей, одна из которых это матрица 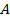 а другая - единичная матрица того же порядка:
а другая - единичная матрица того же порядка:
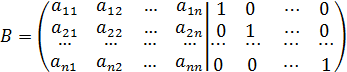
Теперь, используя схему последовательных исключений Гаусса, преобразуем матрицу 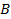 так, чтобы в левой ее части получилась единичная матрица, тогда в правой части будет стоять матрица, обратная к
так, чтобы в левой ее части получилась единичная матрица, тогда в правой части будет стоять матрица, обратная к 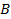 . Преобразовывая матрицу
. Преобразовывая матрицу 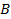 , мы можем умножать все элементы строки матрицы
, мы можем умножать все элементы строки матрицы 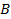 на одно и то же число и складывать соответствующие элементы двух строк.
на одно и то же число и складывать соответствующие элементы двух строк.
Строку матрицы 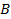 , умноженную каждый раз на свое конкретное число, будем складывать с каждой другой строкой (кроме нее самой) матрицы
, умноженную каждый раз на свое конкретное число, будем складывать с каждой другой строкой (кроме нее самой) матрицы 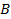 . Так поступим с каждой строкой матрицы
. Так поступим с каждой строкой матрицы 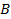 .
.
Мы оставляем не доказанным тот факт, что изложенный алгоритм действительно даст обратную матрицу, заметим только, что этот факт следует из свойств операции умножения матриц.
Пример 2.12. Найти матрицу, обратную к матрице
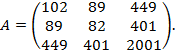
Матрица 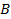 будет иметь вид:
будет иметь вид:

Умножим элементы первой строки матрицы 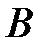 на (-89/102) и прибавим получившиеся значения к соответствующим элементам второй строки; затем умножим первую строку матрицы
на (-89/102) и прибавим получившиеся значения к соответствующим элементам второй строки; затем умножим первую строку матрицы 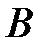 на (-449/102) и сложим с третьей строкой. Первую строку разделим на 102. В результате матрица
на (-449/102) и сложим с третьей строкой. Первую строку разделим на 102. В результате матрица 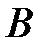 превратится в матрицу
превратится в матрицу 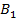 :
:

Умножим элементы второй строки матрицы 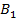 на (-0.87255/4.34314) и прибавим их к соответствующим элементам первой строки; затем вторую строку из
на (-0.87255/4.34314) и прибавим их к соответствующим элементам первой строки; затем вторую строку из 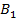 умножим на (-9.22550/4.34314) и сложим с третьей её строкой. Вторую строку матрицы
умножим на (-9.22550/4.34314) и сложим с третьей её строкой. Вторую строку матрицы 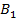 разделим на 4.34314, получим матрицу
разделим на 4.34314, получим матрицу  :
:
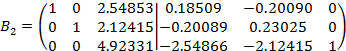
Умножим третью строку из  на (-2.54853/4.92331) и сложим с первой её строкой. Умножим третью строку на (-2.12415/4.92331) и сложим со второй. Разделим третью строку на 4.92331, получим матрицу
на (-2.54853/4.92331) и сложим с первой её строкой. Умножим третью строку на (-2.12415/4.92331) и сложим со второй. Разделим третью строку на 4.92331, получим матрицу 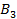 :
:
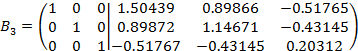
После округлении до тысячных получаем:
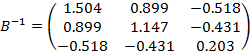
Дата публикования: 2014-11-02; Прочитано: 802 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
