Построение экономико-математической модели задачи

Поскольку в задаче необходимо определить объемы производ­ства для продажи краски, то введем обозначения переменных за­дач:

суточные объемы производства красок для наружных и внут­ренних работ х_н и x_в тонн соответственно.

Критерием достижения поставленной цели, является доход от реализации краски, кото­рый должен быть максимально возможным.

Следовательно, целе­вая функция будет иметь вид:

F()=(2x_н+3x_в) -> max.

Решение любой практической задачи осуществляется в рамках ограниченных ресурсов.

В данном случае необходимо учесть огра­ничения на расход сырья, запасы которого на фабрике не беско­нечны, а также ограничения на спрос краски.

Математически эти ограничения можно записать следующим образом:

0,5x_н+x_в ≤ 3 запасы сырья А,

x_н + 0,5x_в≤ 4 запасы сырья В,

x_в - х_н ≤ 1,5 соотношение спроса на краски,

x_в≤ 2 максимальная величина спроса на краску В.

Объемы производства и соответственно продажи краски не могут принимать отрицательных значений.

Запишем условие неотрицательности переменных:

x_н ≥ 0; x_в ≥ 0

Известно, что план фабрики предусматривает обя­зательный выпуск красок указанных видов, производство которых за всю историю не опускалось ниже, чем

x_н ≥ 0,25; x_в ≥ 0,5

Модель задачи формулируется как:

Определить суточные объемы производства красок который при заданных условиях-ограничениях

0,5x_н+x_в ≤ 3

x_н + 0,5x_в≤ 4

x_в - х_н ≤ 1,5

x_в≤ 2

x_н ≥ 0,25

x_в ≥ 0,5

обеспечивает максимально возможный доход от продажи краски в соответствии с целевой функцией:

F()=(2x_н+3x_в) -> max.

Полученная модель является задачей линейного программирова­ния, так как все входящие в нее функции линейны.

Решение данной задачи возможно с использованием геометрического метода или алге­браического симплексного метода, рассмотренных ниже.

Планирование товарооборота.

Коммерческое предприятие реализует товары нескольких групп:

A j ( j = )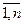

Для реализации этих товаров используются ресурсы с ограниченным объемом: b1 - рабочее время (чел-ч);

b2 ~ площадь залов (м²);

b3 ~ издержки обращения (руб.).

Известны нормы рас­хода каждого вида ресурса на реализацию единицы j-й группы то­вара –

aij, (i = ; j = ).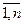

Доход в расчете на единицу товара составляет Cj.

Необходимо составить оптимальный план товарооборота по критерию максимума дохода F (или по другому критерию - мини­мум издержек обращения).