Гармонический осциллятор. Фононы

Для описания классических и квантовых систем часто используют модель гармонического осциллятора. Линейным гармоническим осциллятором называют систему, совершающую одномерное колебательное движение под действием квазиупругой силы . Потенциальная энергия имеет вид: . Примером классического гармонического осциллятора может служить пружинный, математический или физический маятник. Частота собственных колебаний классического гармонического осциллятора 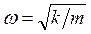, где m – масса частицы. То есть .

Рис. 6.4. Возможные значения энергии для квантового осциллятора

Следовательно, потенциальная энергия равна:

(6.9)

Уравнение Шредингера следует записать в виде:

(6.10)

Только при некоторых значениях параметра Е уравнение (6.10) имеет конечные, однозначные и непрерывные решения (а именно таким условиям должны удовлетворять волновые функции):

(n = 0, 1, 2,...) (6.11)

Таким образом, энергия квантового осциллятора, в отличие от классического, может принимать только дискретные значения. Такая система может переходить из одного состояния в другое при поглощении или излучении порции энергии, равной разнице энергий между этими состояниями.

Учет законов сохранения указывает, что для гармонического осциллятора возможны переходы только между соседними уровнями, то есть по правилу ∆n = 1. Данное условие носит название правило отбора для энергетических переходов. Как следует из формулы (6.11), расстояние между всеми уровнями энергии квантового осциллятора одинаковы и равны . Это значит, что переход из одного состояния в другое происходит при поглощении или испускании одного кванта энергии .

Еще одно отличие квантового осциллятора – это существование энергии нулевых колебаний. Минимальное значение энергии классического осциллятора равно нулю. Минимум энергии квантового осциллятора, называемый энергией нулевых колебаний, отличен от нуля: . Это явление имеет чисто квантовую природу и является прямым следствием соотношения неопределенности Гейзенберга. Если предположить, что квантовая частица опускается на дно потенциальной ямы (то есть ее энергия обнуляется), это означает, что обнуляется и импульс частицы (а следовательно и неопределенность импульса ∆p). Согласно принципу неопределенности ∆x должна стать равной бесконечности, то есть область, в которой частица может перемещаться принимает бесконечно большие размеры, что противоречит факту нахождения частицы в яме конечного размера.

Рассмотрим поведение системы, которую можно описать как гармонический осциллятор. Волновые функции и их квадраты для первых трех состояний показаны на рис. (6.5). Видно, что в состоянии n = 0 наиболее вероятным является нахождение частицы в некотором положении равновесия.

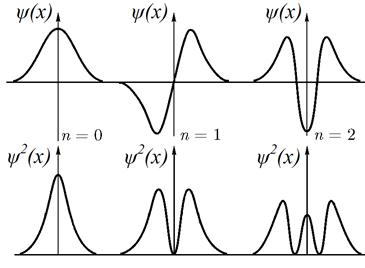
Рис. 6.5. Волновые функции квантового осциллятора

В состоянии n = 1 это положение частицы становится невозможным, так как квадрат волновой функции в этой точке равен нулю. Таким образом, частица в возбужденном состоянии приобретает новое положение равновесия – оно будет там, где квадрат волновой функции максимален.

Достаточно хорошо с помощью теории гармонического осциллятора описываются колебания атомов, которые находятся в узлах в кристаллической решетки. При температуре выше абсолютного 0 К происходят тепловые колебания атомов около положения равновесия. Амплитуда колебаний ионов у большинства кристаллов не превышает 0.01 нм, при этом среднее расстояние между ионами решетки составляет 0.1 ÷ 1 нм. Но движение ионов является весьма сложным. Дело в том, что колеблющиеся частицы связаны между собой силами взаимодействия. Между ионами кристаллической решетки одновременно действуют силы притяжения и отталкивания. Если ионы изобразить в виде шариков, а силы взаимодействия изобразить в виде сжатой или растянутой пружины, то имеется определенное расстояние между ионами, на котором ионы будут находиться в положении равновесия.

Рис. 6.6. Квазиупругая модель кристалла

Если один из ионов вывести из положения равновесия, например, силой F, то его перемещение вызовет соответствующее перемещение соседних ионов. Даже если действие силы прекратится, то выведенные из положения равновесия ионы будут совершать колебания. Эти колебания из-за связей, существующих между ионами, будут передаваться по кристаллу.

В результате в кристалле распространяются колебания, т.е. возникает волна. Волны, достигнув поверхности кристалла, отражаются от нее. Отраженная и исходная волны интерферируют – в кристалле возникает стоячая волна. Это явление аналогично тому, которое происходит в закрепленной с двух сторон струне. В кристалле также устанавливается набор стоячих волн, причем величина каждой длины волны зависит от размеров кристалла и его упругих свойств. Таким образом, природа тепловых упругих волн в кристалле аналогична природе звуковых волн, поэтому их еще называют акустическими. Интервал частот тепловых волн очень широк – 10² ÷ 10¹³ Гц.

Как следует из квантовой механики, энергия колебаний ионов должна быть дискретной, т.е. квантована. Квант энергии тепловых колебаний ионов кристаллической решетки называется фононом и равен:

(6.12)

где ω – частота колебаний ионов.

Фононы, т.е. распространяющиеся в кристалле элементарные возбуждения, наделяются свойством частиц и называются квазичастицами. Они являются элементарными носителями колебательного движения в системе реальных частиц, входящих в состав кристаллической решетки и связанных между собой взаимодействием. По аналогии с квантами света – фотонами, можно задать импульс фонона:

(6.13)

где 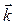– волновой вектор, . Учитывая особые свойства фонона, его импульс также имеет необычный смысл, поэтому в случае фононов говорят о квазиимпульсе.

Фонон может существовать только в кристалле и в отличие от реальных частиц никогда не возникнет в вакууме. В пределах кристаллической решетки может образоваться неограниченное количество фононов. Их можно рассматривать как так называемый «фононный газ». Так же, как атомы реального газа, в процессе движения в кристалле фононы сталкиваются между собой или с дефектами кристаллической решетки, и при этом могут передать решетке порцию импульса. Это осуществляется, например, при возникновении безызлучательных явлений в кристалле. Эти процессы, по сути, являются такими же переходами электронов между энергетическими уровнями, как в атомах (смотри лекцию 3). Только в случае участия фотона, от него электрон в атоме получает импульс, а следовательно и энергию, необходимую для перехода на другой уровень. В безызлучательном процессе энергию светового кванта электрон не получает, и по законам сохранения его переход вверх по уровням энергии был бы не возможен. Однако такие процессы протекают, и объяснить их можно только тем, что энергия колебательных движений кристаллической решетки (т.е. энергия фонона) может быть использована в качестве недостающей порции.