Основные законы гемодинамики

Гемодинамика - один из разделов биомеханики, изучающий законы движения крови по кровеносным сосудам. Задача гемодинамики - установить взаимосвязь между основными гемодинамическими показателями, а также их зависимость от физических параметров крови и кровеносных сосудов.

К основным гемодинамическим показателям относятся давление и скорость кровотока.

Давление - это сила, действующая со стороны крови на сосуды, приходящаяся на единицу площади: Р = F / S. Различают объемную и линейную скорости кровотока. Объемной скоростью Q называют величину, численно равную объему жидкости, перетекающему в единицу времени через данное сечение трубы: , единица измерения (м³ / с).

Линейная скорость представляет путь, проходимый частицами крови в единицу времени: , единица измерения (м / с). Поскольку линейная скорость неодинакова по сечению трубы, то в дальнейшем речь будет идти только о линейной скорости, средней по сечению.

Линейная и объемная скорости связаны простым соотношением Q = VS, где S - площадь поперечного сечения потока жидкости.

Так как жидкость несжимаема (то есть плотность ее всюду одинакова), то через любое сечение трубы и в единицу времени протекают одинаковые объемы жидкости:

Q = VS = Сonst (3 ).

Это называется условием неразрывности струи. Оно вытекает из закона сохранения массы для несжимаемой жидкости. Уравнение неразрывности струи относится в равной мере к движению всякой жидкости, в том числе и вязкой. При описании физических законов течения крови по сосудам вводится допущение, что количество циркулирующей крови в организме постоянно. Отсюда следует, что объемная скорость кровотока в любом сечении сосудистой системы также постоянна: Q = const.

В реальных жидкостях (вязких) по мере движения их по трубе потенциальная энергия расходуется на работу по преодолению внутреннего трения, поэтому давление жидкости вдоль трубы падает. Для стационарного ламинарного течения реальной жидкости в цилиндрической трубе постоянного сечения справедлива формула (закон) Гагена—Пуазейля:

, (4)

где ∆Р = Р₁ - Р₂ - падение давления, то есть разность давлений у входа в трубу Р₁и на выходе из нее Р₂ на расстоянии l. Величина

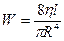(5)

называется гидравлическим сопротивлением сосуда. Тогда закон Пуазейля можно записать в виде:

∆Р=QW (6).

Из закона Пуазейля следует, что падение давления крови в сосудах зависит от объемной скорости кровотока и в сильной степени от радиуса сосуда. Так, уменьшение радиуса на 20 % приводит к увеличению падения давления более чем в 2 раза. Даже небольшие изменения просветов кровеносных сосудов сильно сказываются на падении давления. Не случайно основные фармакологические средства нормализации давления направлены прежде всего на изменение просвета сосудов.

Границы применимости закона Пуазейля: 1) ламинарное течение; 2) гомогенная жидкость; 3) прямые жесткие трубки; 4) удаленное расстояние от источников возмущений (от входа, изгибов, сужений).

Рассмотрим гемодинамические показатели в разных частях сосудистой системы.

Гидравлическое сопротивление.

Гидравлическое сопротивление w в значительной степени зависит от радиуса сосуда. Отношения радиусов для различных участков сосудистого русла:

R_аорт:R_ар:R_кап=3000:500:1.

Поскольку гидравлическое сопротивление в сильной степени зависит от радиуса сосуда w~1/R⁴, то можно записать соотношение:

w_кап > w_ар > w_аорт.

Линейная скорость кровотока.

Рассмотрим закон неразрывности (3). Площадь суммарного просвета всех капилляров в 500 - 600 раз больше поперечного сечения аорты. Это означает, что V_кап ≈ 1/500 V_aopт. Именно в капиллярной сети при медленной скорости движения происходит обмен веществ между кровью и тканями.

На рис. 9.4 приведена кривая распределения линейных ско­ростей вдоль сосудистой системы.

Рис. 9.4. Линейная скорость в различных участках сосудистого русла

Распределение среднего давления.

При сокращении сердца давление крови в аорте испытывает колебания. Сейчас будет речь идти о среднем давлении за период. Среднее давление может быть оценено по формуле

.

Падение среднего давления крови вдоль сосудов может быть описано законом Пуазейля (6). Сердце выбрасывает кровь под средним давлением Р_оср. По мере продвижения крови по сосудам среднее давление падает. Поскольку Q=const, а w_кап > w_арт > w_аорт, то для средних значених давлений:

∆Р_кап > ∆Р_арт > ∆Р_аорт.

В крупных сосудах среднее давление падает всего на 15 %, а в мелких на 85 %. Это означает, что большая часть энергии, затрачиваемой левым желудочком сердца на изгнание крови, расходуется на ее течение по мелким сосудам.

Распределение давления (превышение над атмосферным) в различных отделах сосудистого русла представлено на рис. 9.5. Отрицательное значение давления означает, что оно несколько ниже атмосферного.

Рис. 9.5. Распределение давления (превышение над атмосферным) в различных участках сосудистого русла (штриховкой обозначена область колебания давления, пунктиром - среднее давление);

1 - давление в аорте, 2 - в крупных артериях, 3 - в мелких артериях,

4 - в артериолах, 5 - в капиллярах