 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Первообразная функции комплексных переменных
|
|
Функция 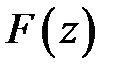 называется первообразной функции
называется первообразной функции 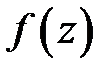 в области в области
в области в области 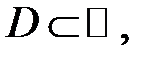 если
если 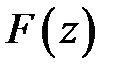 дифференцируема в
дифференцируема в 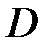 и
и 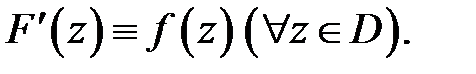
Теорема 1. Если однозначная функция 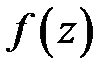 дифференцируема в односвязной области
дифференцируема в односвязной области 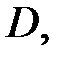 то она имеет первообразную в этой области. Одной из первообразных является интеграл
то она имеет первообразную в этой области. Одной из первообразных является интеграл 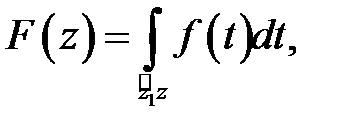 где
где 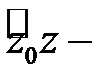 любой кусочно-гладкий путь, соединяющий фиксированную точку
любой кусочно-гладкий путь, соединяющий фиксированную точку 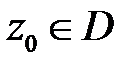 с текущей точкой
с текущей точкой 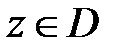 . Все остальные первообразные имеют вид
. Все остальные первообразные имеют вид 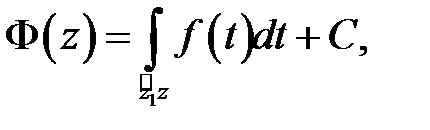 где
где 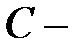 произвольная комплексная постоянная.
произвольная комплексная постоянная.
Доказательство этой теоремы проводится так же, как и в действительном анализе. Используя эту теорему, нетрудно доказать следующие утверждения.
1. Если функция 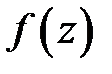 аналитична в односвязной области
аналитична в односвязной области 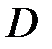 и
и 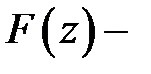 её первообразная в
её первообразная в 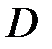 , то справедлива формула Ньютона-Лейбница
, то справедлива формула Ньютона-Лейбница
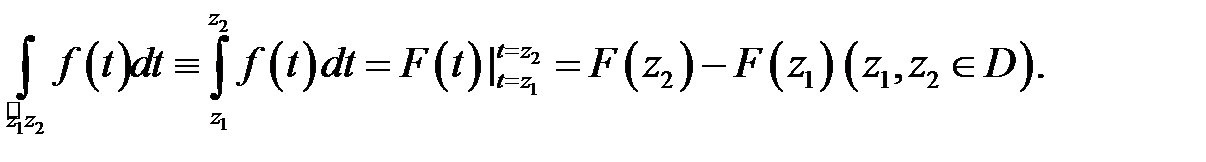
2. Если функция 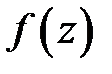 аналитична в односвязной области
аналитична в односвязной области 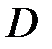 и
и 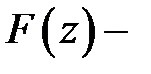 её первообразная в
её первообразная в 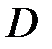 , то справедлива формула интегрирования по частям
, то справедлива формула интегрирования по частям
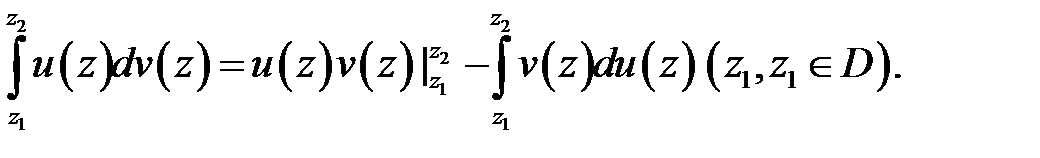
Замена переменных в интегралах от функции комплексного переменного аналогична случаю функции действительного переменного. Пусть аналитическая функция 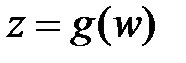 отображает взаимно однозначно кусочно-гладкий контур
отображает взаимно однозначно кусочно-гладкий контур 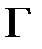 в плоскости
в плоскости 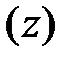 на контур
на контур 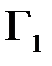 в плоскости
в плоскости 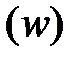 . Тогда
. Тогда
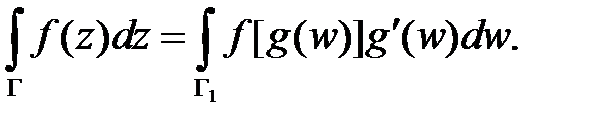
Замечание 2. Интегралы от элементарных однозначных функций в односвязных областях вычисляются по тем же формулам, что и в действительном анализе. Если же область 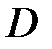 неодносвязна, то это правило может нарушаться. Для вычисления интеграла от многозначной функции указывается, какая именно однозначная ветвь ее берется. Это достигается заданием значения многозначной функции в некоторой точке контура интегрирования. Если контур интегрирования
неодносвязна, то это правило может нарушаться. Для вычисления интеграла от многозначной функции указывается, какая именно однозначная ветвь ее берется. Это достигается заданием значения многозначной функции в некоторой точке контура интегрирования. Если контур интегрирования 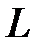 замкнут, то начальной точкой
замкнут, то начальной точкой 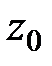 пути интегрирования считается та, в которой задано значение подынтегральной функции. Рассмотрим примеры (пример взяты из пособия Острая О.В. “Теория функций комплексного переменного”.- Оренбург, 2008).
пути интегрирования считается та, в которой задано значение подынтегральной функции. Рассмотрим примеры (пример взяты из пособия Острая О.В. “Теория функций комплексного переменного”.- Оренбург, 2008).
Пример 3. Вычислить 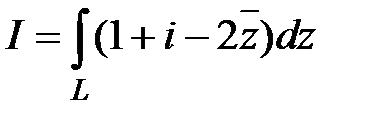 по кривой
по кривой 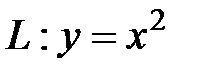 , соединяющей точки
, соединяющей точки 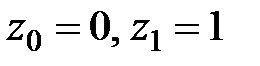 .
.
Решение. Для параболы 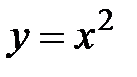 имеем
имеем 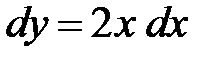 ,
, 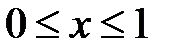 . По формуле (48)
. По формуле (48) 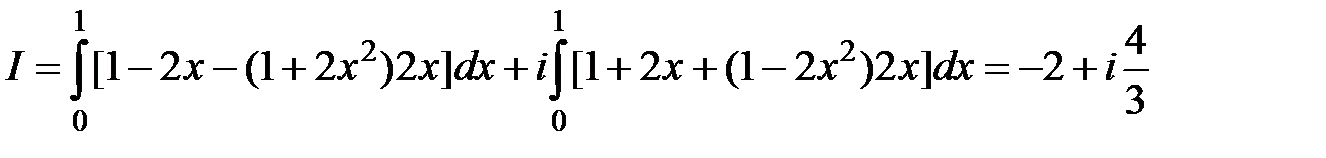 .
.
Пример 4. Вычислить 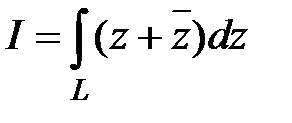 , где
, где 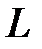 – дуга окружности
– дуга окружности 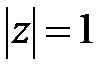 ,
, 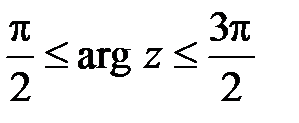 .
.
Решение. Положим 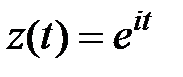 ,
, 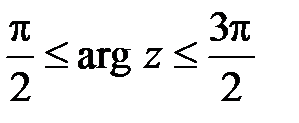 . Тогда
. Тогда 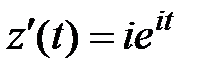 , и по формуле (49) находим:
, и по формуле (49) находим:
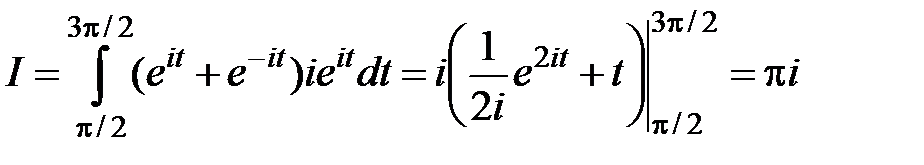 .
.
Пример 5. Вычислить 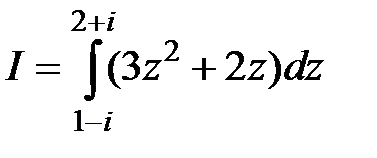 .
.
Решение. Так как подынтегральная функция 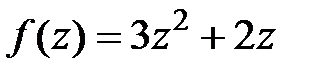 аналитична всюду, то по (50) найдем:
аналитична всюду, то по (50) найдем: 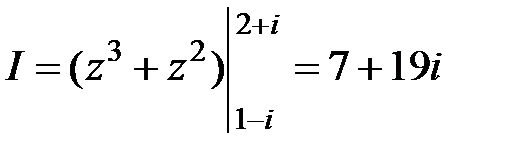 .
.
Пример 6. Вычислить 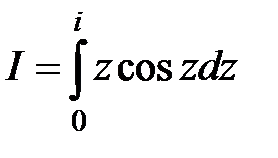 .
.
Решение. Функции 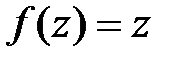 и
и 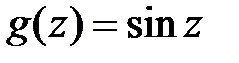 аналитичны всюду. По формуле (51) получим:
аналитичны всюду. По формуле (51) получим:
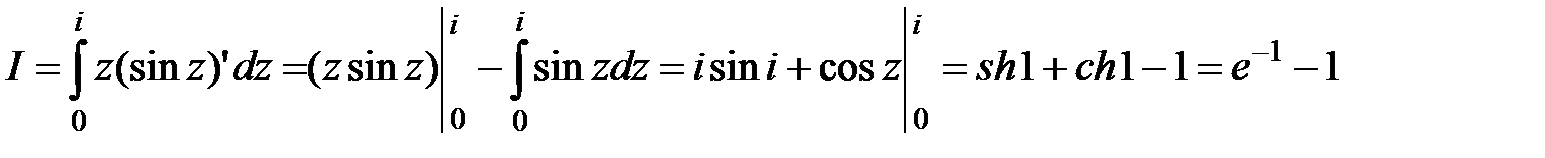 .
.
Пример 7. Вычислить 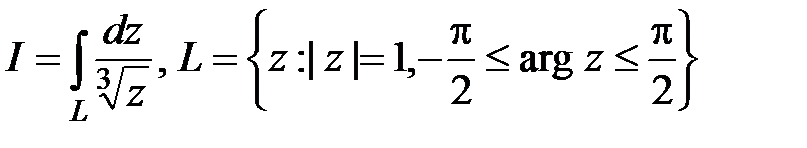 ,
, 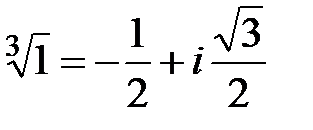 .
.
Решение. Функция 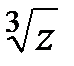 является многозначной:
является многозначной: 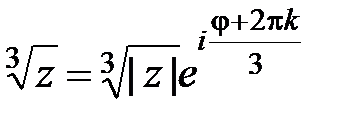 ,
, 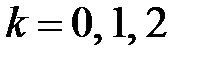 ;
; 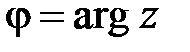 . Условию
. Условию 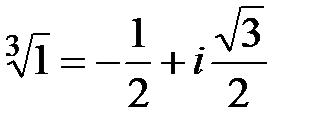 удовлетворяет та однозначная ветвь этой функции, для которой
удовлетворяет та однозначная ветвь этой функции, для которой 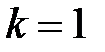 . Действительно, при
. Действительно, при 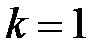 (и так как
(и так как 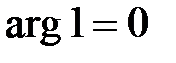 )
) 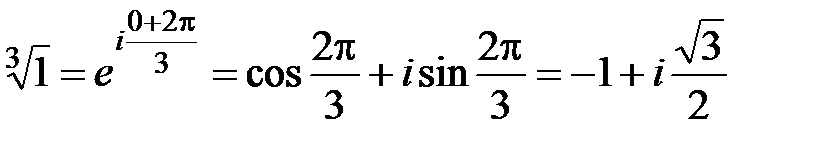 . Полагая теперь
. Полагая теперь 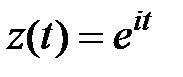 ,
, 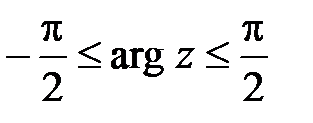 на кривой
на кривой 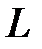 , находим
, находим 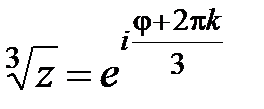 ,
, 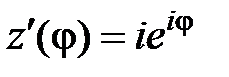 и, следовательно,
и, следовательно, 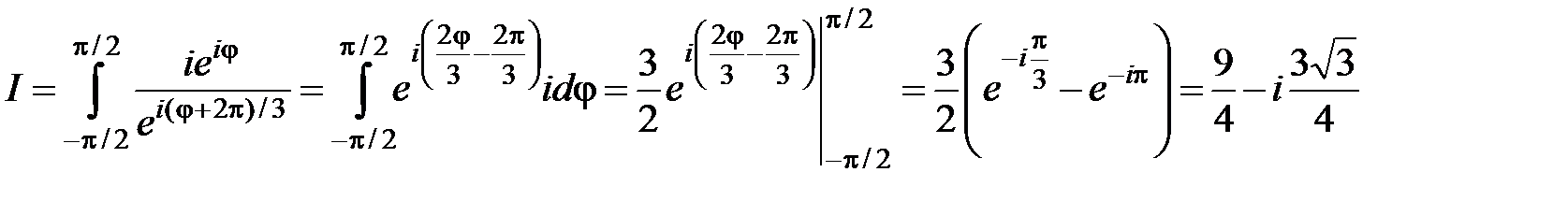 .
.
Лекция 8. Ряды в комплексной области. Степенные ряды. Теорема Абеля. Ряды Тейлора и Лорана
Пусть дана функциональная последовательность 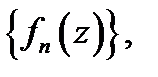 состоящая из комплексных функций (
состоящая из комплексных функций (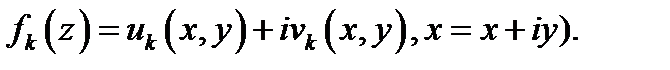 Тогда формальная сумма бесконечного числа слагаемых:
Тогда формальная сумма бесконечного числа слагаемых:
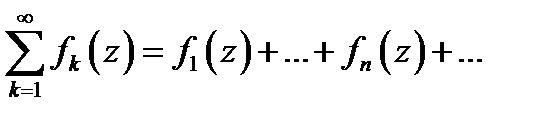
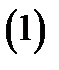
называется рядом, построенным по указанной функциональной последовательности. В частности, если все 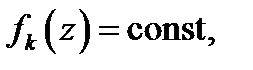 то ряд будет числовым. При этом
то ряд будет числовым. При этом 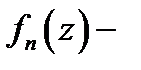 общий член ряда (1), а
общий член ряда (1), а 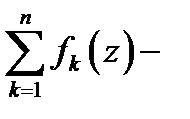 его
его 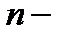 я частичная сумма. Множество
я частичная сумма. Множество
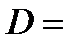 {все
{все 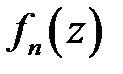 имеют смысл}
имеют смысл}
называется областью определения ряда (1).
Определение 1. Говорят, что ряд (1) сходится в точке 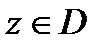 к сумме
к сумме 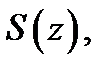 если существует конечный предел
если существует конечный предел 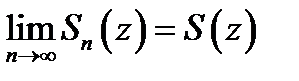 его частичных сумм. Это эквивалентно высказыванию
его частичных сумм. Это эквивалентно высказыванию 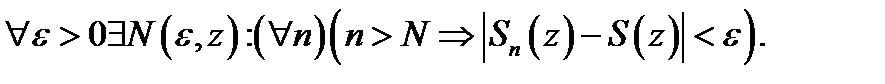 Если здесь номер
Если здесь номер 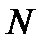 не зависит от
не зависит от 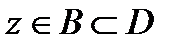 (т.е.
(т.е. 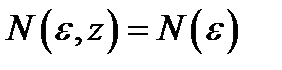 ), то говорят, что ряд (1) сходится равномерно по
), то говорят, что ряд (1) сходится равномерно по 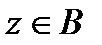 (или равномерно на множестве
(или равномерно на множестве 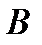 ).
).
Это определение фактически не отличается от аналогичного определения в действительном анализе. Поэтому здесь также справедливы следующие утверждения.
1. Если ряд (1) сходится в точке 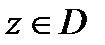 , то его общий член
, то его общий член 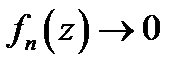 при
при 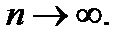
2. Если “модульный ряд” 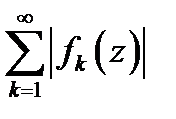 сходится, то сходится и сам ряд (1) (в этом случае говорят, что ряд (1) сходится абсолютно; если ряд (1) сходится, а его “модульный ряд” расходится, то говорят, что (1) сходится условно).
сходится, то сходится и сам ряд (1) (в этом случае говорят, что ряд (1) сходится абсолютно; если ряд (1) сходится, а его “модульный ряд” расходится, то говорят, что (1) сходится условно).
Для нахождения области абсолютной сходимости ряда (1) и области его равномерной сходимости надо применить известные признаки сходимости (Даламбера, Коши, интегральный признак, признак Вейерштрасса) к действительному знакоположительному ряду 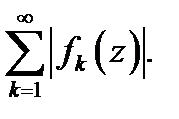 При этом все свойства равномерно сходящихся действительных рядов рядов переносятся и на комплексные ряды. Эти свойства следующие.
При этом все свойства равномерно сходящихся действительных рядов рядов переносятся и на комплексные ряды. Эти свойства следующие.
3. Если ряд (1) состоит из непрерывных на множестве 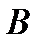 слагаемых
слагаемых 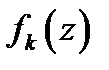 и сходится к сумме
и сходится к сумме 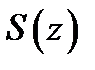 равномерно на множестве
равномерно на множестве 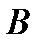 , то его сумма
, то его сумма 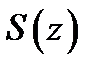 непрерывна на
непрерывна на 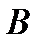 .
.
4. Если ряд (1) сходится равномерно на ограниченной кусочно- гладкой кривой 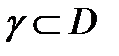 и все его члены непрерывны на
и все его члены непрерывны на 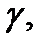 то ряд (1) можно интегрировать на
то ряд (1) можно интегрировать на 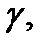 т.е.
т.е.
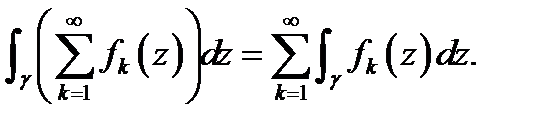
5. Если все члены ряда (1) аналитичны в ограниченной односвязной области 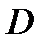 и ряд (1) сходится равномерно в замкнутой области
и ряд (1) сходится равномерно в замкнутой области  то его сумма
то его сумма 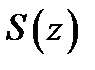 аналитична в
аналитична в 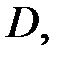 причем
причем
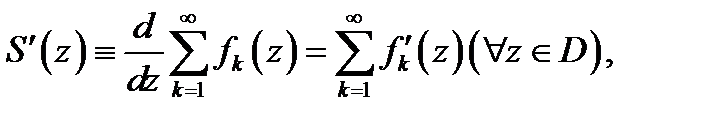
а ряд из производных будет сходиться равномерно по 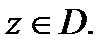
Дата публикования: 2014-11-04; Прочитано: 2561 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
