Обернена матриця

Матриця 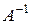називається оберненоюдо матриці 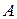, якщо виконується умова

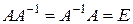. (3.1)

Теорема 3.1. Будь-яка невироджена матриця має обернену.

Доведення. Знайдемо добуток матриць 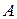і :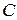

.

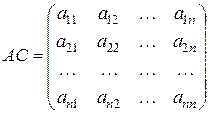
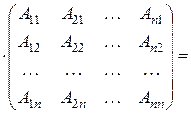
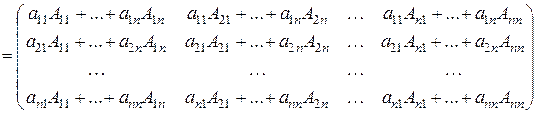З властивостей визначників 9, 10 отримаємо

= = ,

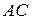
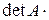
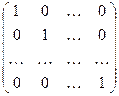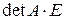тобто

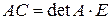. (3.2)

Аналогічно доводимо, що

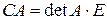. (3.3)

Рівності (3.2), (3.3) перепишемо у вигляді

, , .

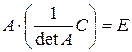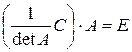Порівнюючи отримані результати з означенням (3.1), робимо висновок:

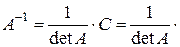
. (3.4)

Властивості оберненої матриці:

1. ;

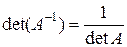2. ;

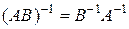3. .

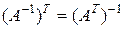Приклад 3.1. Вияснити,чи існує обернена матриця 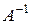до матриці

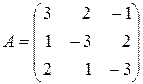
і, якщо існує, то знайти її.

Розв’язок. Знаходимо визначник матриці :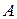

.

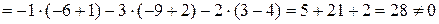Отже, дана матриця невироджена, і 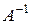існує.

Згідно формули (3.4)

.

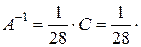
Знайдемо алгебраїчні доповнення 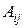елементів даної матриці:

; ;

; ;

; ;

; ;

.

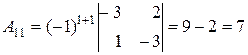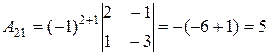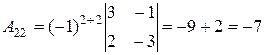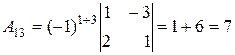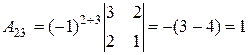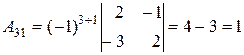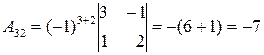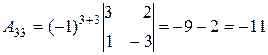Тоді

.

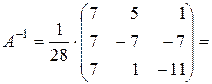
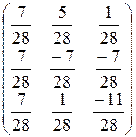Перевірка:

=

= .

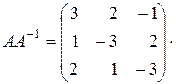
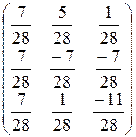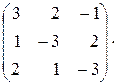
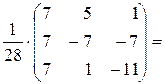
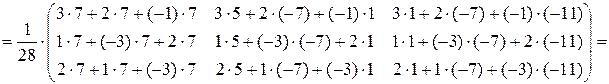
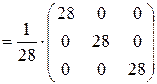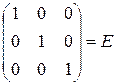Також

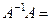
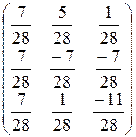
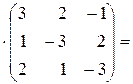
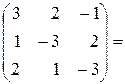
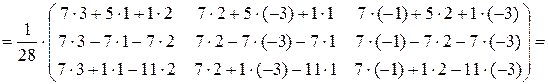
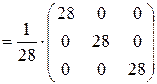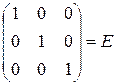= . t