 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Екстремум функції
|
|
Точка 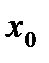 з області визначення функції
з області визначення функції 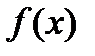 називається точкою мінімуму цієї функції, якщо існує такий
називається точкою мінімуму цієї функції, якщо існує такий 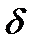 - окіл
- окіл 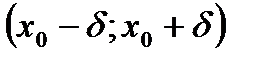 точки
точки 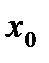 , що для всіх
, що для всіх 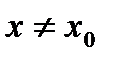 з цього околу виконується нерівність
з цього околу виконується нерівність 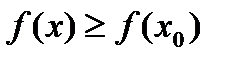 .
.
Точка 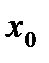 з області визначення функції
з області визначення функції 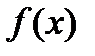 називається точкою максимуму цієї функції, якщо існує такий
називається точкою максимуму цієї функції, якщо існує такий 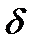 - окіл
- окіл 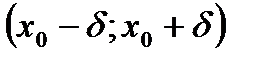 точки
точки 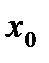 , що для всіх
, що для всіх 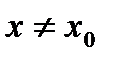 з цього околу виконується нерівність
з цього околу виконується нерівність 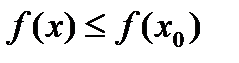 .
.
Точки мінімуму і максимуму функції називаються точками екстремуму даної функції, а значення функції в цих точках – мінімумом і максимумом (або екстремумами) функції.
Точками екстремуму можуть бути тільки критичні точки функції. Якщо при переході через критичну точку 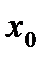 похідна
похідна 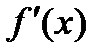 змінює знак, то функція
змінює знак, то функція 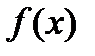 має в точці
має в точці 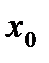 екстремум: мінімум тоді, коли похідна змінює знак з мінуса на плюс, і максимум, - коли з плюса на мінус. Якщо ж при переході через критичну точку
екстремум: мінімум тоді, коли похідна змінює знак з мінуса на плюс, і максимум, - коли з плюса на мінус. Якщо ж при переході через критичну точку 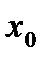 похідна
похідна 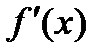 не змінює знака, то функція
не змінює знака, то функція 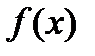 в точці
в точці 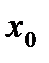 не має екстремуму.
не має екстремуму.
Правило знаходження екстремумів функції 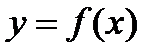
1. Знайти область визначення функції;
2. Знайти похідну функції 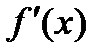 ;
;
3. Знайти критичні точки функції;
4. Нанести критичні точки на область визначення функції;
5. Визначити знак похідної 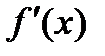 на кожному з отриманих проміжків;
на кожному з отриманих проміжків;
6. Визначити наявність та характер точок екстремуму;
7. Обчислити значення функції в точках екстремуму.
129. Дослідіть на екстремум такі функції:
1) 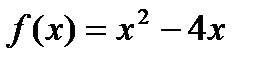 ; 2)
; 2) 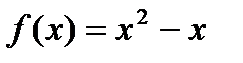 ;
;
3) 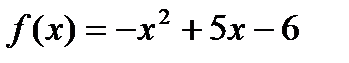 ; 4)
; 4) 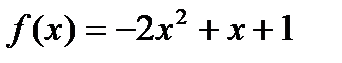 ;
;
5) 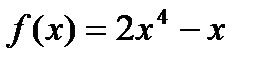 ; 6)
; 6) 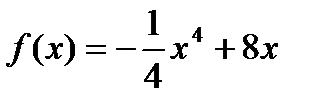 ;
;
7) 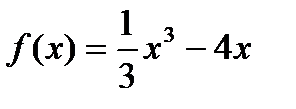 ; 8)
; 8) 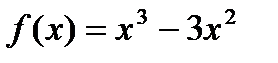 ;
;
9) 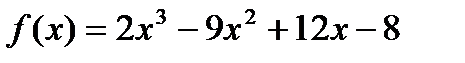 ; 10)
; 10) 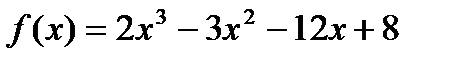 ;
;
11) 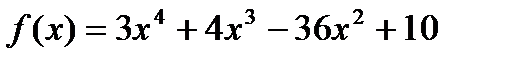 ; 12)
; 12) 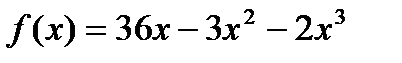 ;
;
13) 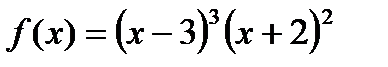 ; 14)
; 14) 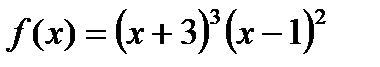 ;
;
15)  ; 16)
; 16) 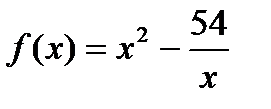 ;
;
17) 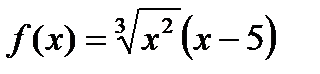 ; 18)
; 18) 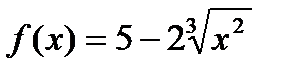 ;
;
19) 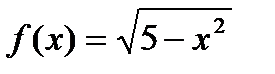 ; 20)
; 20) 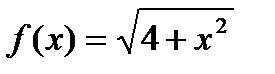 .
.
130. Дослідіть функції на монотонність та екстремум:
1) 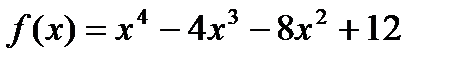 ; 2)
; 2) 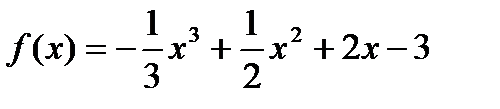 ;
;
3) 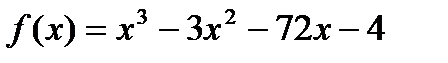 ; 4)
; 4) 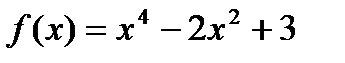 ;
;
5) 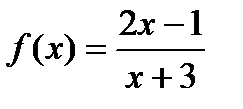 ; 6)
; 6) 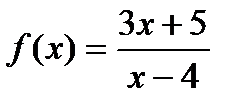 ;
;
7) 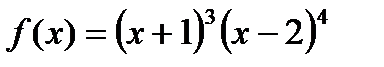 ; 8)
; 8) 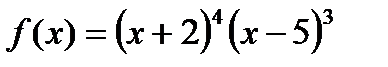 ;
;
9) 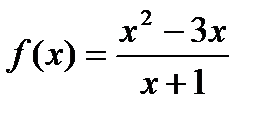 ; 10)
; 10) 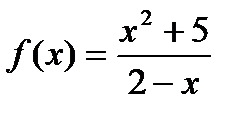 ;
;
11) 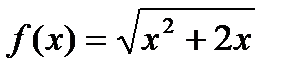 ; 12)
; 12) 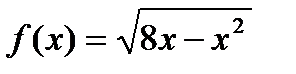 ;
;
13) 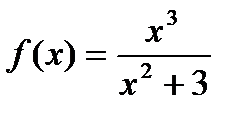 ; 14)
; 14) 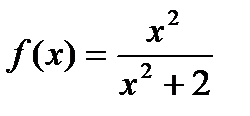 ;
;
15) 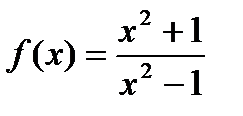 ; 16)
; 16) 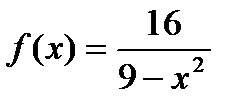 .
.
131. З’ясуйте, при яких значеннях параметра 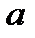 функція
функція 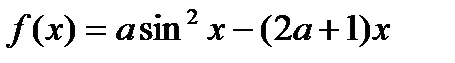 :
:
1) не має критичних точок;
2) не має екстремумів.
до змісту
Дата публикования: 2014-11-04; Прочитано: 628 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
