Химическое равновесие. Как уже указывалось, химические реакции идут в обе стороны с одновременным образованием конечных продуктов и исходных веществ

Как уже указывалось, химические реакции идут в обе стороны с одновременным образованием конечных продуктов и исходных веществ. Если процесс химического реагирования длится достаточно долго, то между исходными и конечными продуктами реакции устанавливается динамическое равновесие. Так, тело, в разных местах которого поддерживается разная, но постоянная во времени температура, находится в стационарном состоянии. Если тело изолировать от внешней среды, то постепенно температура его во всем объеме выравнивается и наступает равновесное состояние. Таким образом, стационарное состояние определяется внешними условиями, а равновесие – внутренними причинами. Условия равновесия описываются с помощью функций состояния. В соответствии со вторым законом термодинамики, для функции состояния энтропии можно записать условие равновесия идеального обратимого процесса

ds – dQ/T = dQ’/T, (58)

где dQ — теплота из внешней среды; dQ' — теплота реагиро­вания внутри системы. При V, s = const условие химического равновесия имеет вид

. (59)

Внутренняя энергия U в этом случае называется термодина­мическим потенциалом, сопряженным с параметрами V и s. Если использовать вместо V и s другие термодинамические пары, то можно получить при равновесии следующее равенство:

, (60)

где Н=U+pV — энтальпия; F=U—Ts — изохорно-изотермический потенциал (энергия Гельмгольца); G = Н—Ts — изобарно-изотермический потенциал (энергия Гиббса). Отсюда сле­дует, что условие равновесия одинаково для всех типов про­цессов (изотермических, изобарических и др.).

В зависимости от условий (температуры, давления) равно­весие смещается в сторону исходных веществ или в сторону продуктов распада. Известно правило, называемое принципом Ле-Шателье-Брауна. В соответствии с этим принципом при изменении условий, в которых происходит реакция, равнове­сие смещается так, чтобы противодействовать изменению этих условий. Например, при горении прямая реакция идет с выделением теплоты, а обратная — с поглощением; в этом случае при повышении температуры в системе равновесие смещается в сторону исходных веществ, тепловыделение уменьшается, при понижении температуры равновесие сме­щается в сторону продуктов реакции. При не очень высоких температурах эти смещения незначительны.

Давление воздействует на положение равновесия, когда реакция протекает с изменением объема газов. В этом случае при повышении давления равновесие смещается в сторону уменьшения объема, а при понижении давления — в сторону увеличения объема. Так, в реакции

2Н₂ + О₂ = 2Н₂О

с ростом давления равновесная полнота реагирования водо­рода с кислородом повышается, при уменьшении давления увеличивается равновесный распад водяного пара.

Принцип Ле-Шателье-Брауна показывает качественный характер смещения равновесия, но не позволяет провести ко­личественные расчеты равновесного состава. Расчет равновесного состава является очень трудной задачей. Здесь мы укажем только общие положения такого расчета и поясним некоторые зависимости, необходимые для понимания процес­сов горения.

Пусть идеальная газовая смесь имеет температуру Т₀,при которой известен ее состав, и объем V; в процессе реагирова­ния смесь не обменивается массой с окружающей средой; температура смеси изменяется от Т₀ до Т, при этом устанав­ливается новый равновесный состав. Перепишем уравнение (55) в следующем виде:

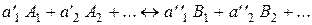. (61)

С приближением к условию (60), т. е. при стремлении термодинамической системы к равновесию, для реакции (61) можно записать

, (62)

где 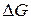– изменение изобарно-изотермического потенциала в реакции при стандартном давлении (1,01·10⁴ Па) и темпера­туре Т; — изменение энтальпии, равное теплоте реакции Q_p при постоянном давлении; — изменение энтропии в реакции; и 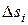— теплота образования и энтропия исходных веществ и продуктов реакции при стан­дартном давлении и температуре Т; х_А, х_А, …; … — относительные молярные концентрации исходных веществ и продуктов реакции (см. (57), (54)).

К_х называется константой равновесия по относительным молярным концентрациям. Она зависит от давления и темпе­ратуры. Выражение (62) есть закон действующих масс (термодинамический): при равновесии связь между массами участвующих в прямой и обратной реакциях веществ определяется константой равновесия.

Запишем выражение (62) в виде

. (63)

Кроме константы равновесия К_х, используют константы равновесия по парциальным давлениям К_р и молярным концентрациям К_с:

, (64)

. (65)

3.2.3.1.3. Кинетический закон действующих масс

Впредыдущих разделах были рассмотрены химические реакции с точки зрения термодинамики. При этом считалось, что равновесные концентрации в реакциях горения устанавливались мгновенно, и время из рассмотрения исключалось. Для многих практических задач такой подход правомерен, однако имеются задачи, когда необходим анализ химических процессов в их временном развитии. Скорости и механизмы механических процессов, законы их протекания во времени изучает химическая кинетика.

Равновесное состояние химический реакции вовсе не означает, что реакция прекратилась. В действительности реакция протекает непрерывно, но с одинаковой скоростью в обоих направлениях. Общее представление о скорости реакции было рассмотрено в ранее. Скорость зависит от концентрации реагентов и температуры. При постоянной температуре скорости прямой w" и обратной w" реакций пропорциональны произведениям концентраций реагентов, возведенных в целочисленные степени (равные стехиометрическим коэффициентам):

; . (66)

Коэффициенты пропорциональности k’ и k’’, зависящие от температуры и химической природы реагирующих веществ (ноне от концентраций), называют константами скоростей. Константа скорости — это скорость реакции, которая была бы при условии, что концентрации всех реагентов равны еди­нице, во все время реагирования.

Скорость реакции пропорциональна числу столкновений молекул реагирующих веществ в единицу времени, а число столкновений в свою очередь пропорционально произведению концентрации; этим элементарно обосновывается кинетический закон действующих масс, который можно записать в виде

. (67)

По мере расходования в процессе реагирования исходных реагентов скорость прямой реакции будет уменьшаться, а скорость обратной — увеличиваться, и наступит момент, когда w’ = w’’ и w = 0. Мы опять пришли к понятию равновесного состояния, но теперь с позиции кинетики: равновесие — это равенство скоростей прямой и обратной реакций. Из (67) при условии равновесия следует

, (68)

что соответствует определению константы равновесия по кон­центрациям (см. (65)).