Поверхности второго порядка

Поверхности второго порядка – это поверхности, которые в декартовой системе координат определяются алгебраическими уравнениями второго порядка

(4.22)

Геометрическое исследование поверхностей второго порядка проведем по заданным уравнениям с помощью метода параллельных сечений.

1. Эллипсоид. Эллипсоидом называется поверхность, которая в некоторой декартовой системе координат определяется каноническим уравнением

(4.23)

Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями z = h.

(4.24)

Если 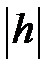> c, то уравнение (4.24) определяет мнимый эллипс. Если 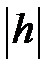= c, то уравнение (4.24) определяет две точки с координатами (0;0;с), (0;0;−с). Если 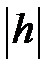< c, то уравнение (4.24) определяет эллипс

полуоси которого при уменьшении h возрастают и принимают наибольшие значения при h = 0. Аналогичная картина получается и при сечении дру­гими координатными плоскостями (рис. 39).

x

y

z

a

b

c

Рис. 39.

Величины a, b, c называются полуосями эллипсоида. В случае a = b = c эллипсоид является сферой.

2. Однополостный гиперболоид. Однополостным гиперболоидом называется поверхность, которая в некоторой декартовой системе координат определяется каноническим уравнением

(4.25)

Установим геометрический вид однополостного гиперболоида. Для этого рассмотрим сечения данного гиперболоида плоскостями z = h.

(4.26)

Уравнение (4.26) определяет эллипс.

полуоси которого при увеличении h возрастают и принимают наименьшие значения при h = 0. При сечении координатными плоскостями x = 0 и y = 0 получаем соответственно уравнения

из которых следует, что в сечениях получаются гиперболы (рис. 40).

z

x

b

a

y

Рис. 40.

3. Двуполостный гиперболоид. Двуполостным гиперболоидом называется поверхность, которая в некоторой декартовой системе координат определяется каноническим уравнением

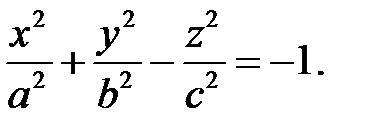(4.27)

Установим геометрический вид двуполостного гиперболоида. Для этого рассмотрим сечения данного гиперболоида плоскостями z = h.

(4.28)

Если 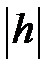< c, то уравнение (4.28) определяет мнимый эллипс. Если 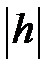= c, то уравнение (4.24) определяет две точки с координатами (0;0;с), (0;0;−с). Если 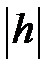> c, то уравнение (4.24) определяет эллипс

полуоси которого при увеличении h возрастают. При сечении координатными плоскостями x = 0 и y = 0 получаем соответственно уравнения

из которых следует, что в сечениях получаются гиперболы. Таким обра­зом, двуполостный гиперболоид состоит из двух отдельных «полостей», каждая из которых имеет вид бесконечной выпуклой чаши (рис. 41).

x

y

z

c

- c

Рис. 41.

4. Эллиптический параболоид. Эллиптическим параболоидом называется поверхность, которая в некоторой декартовой системе координат определяется каноническим уравнением

(4.29)

где p > 0 и q > 0.

Установим геометрический вид эллиптического параболоида. Для этого рассмотрим сечения данного гиперболоида (4.29) плоскостями z = h.

(4.30)

Если 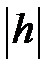< 0, то уравнение (4.28) определяет мнимый эллипс. Если 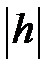= 0, то уравнение (4.30) определяет точку с координатами (0;0;0). Если 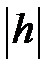> 0, то уравнение (4.30) определяет эллипс

полуоси которого при увеличении h возрастают. При сечении координатными плоскостями x = 0 и y = 0 получаем соответственно уравнения

z

из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат. Таким образом, эллип­тический параболоид имеет вид бесконечной выпуклой чаши (рис. 42).

x

y

Рис. 42.

5. Гиперболический параболоид. Гиперболическим параболоидом называется поверхность, которая в некоторой декартовой системе координат определяется каноническим уравнением

(4.31)

где p > 0 и q > 0.

Установим геометрический вид гиперболического параболоида. Для этого рассмотрим сечения данного гиперболоида (4.31) плоскостями z = h.

из которых следует, что в сечениях получаются гиперболы с действительными осями, параллельными оси Ox при h > 0; и гиперболы с действительными осями, параллельными оси Oy при h < 0. При h = 0 гипербола вы­рождается в пару пересекающихся прямых. При сечении координатной плоскостью y = 0

получаем уравнение

(4.32)

из которого следует, что в сечении получается парабола, симметричная относительно оси Oz, с вершиной в начале координат, которая направлена вверх. При сечении координатной плоскостью y = h получаются также направленные вверх параболы

При сечении координатной плоскостью x = h получаются направленные вниз параболы

z

Вершины этих парабол лежат на направленной вверх параболе (4.32), (рис. 43).

x

y

Рис. 43.

6. Конус второго порядка. Конусом второго порядка называется поверхность, которая в некоторой декартовой системе координат определяется каноническим уравнением

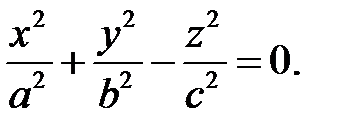(4.33)

Установим геометрический вид конуса второго порядка (рис. 44). Для этого рассмотрим сечения данного гиперболоида (4.33) плоскостями z = h.

(4.34)

Уравнение (4.34) определяет эллипс

полуоси которого при увеличении h возрастают. При h = 0 поверхность конуса вырождается в точку (0;0;0). При сечении координатными плоскостями x = 0 и y = 0 получаются соответственно уравнения пары прямых

Конус второго порядка обладает замечательным свойством. Если некоторая точка M, отличная от начала координат, лежит на этой поверхности, то и все точки прямой, которая проходит через начало координат и точку M, также лежат на поверхности.

Действительно, пусть M (x ₀, y ₀, z ₀), тогда параметрическое уравнение прямой OM

Произвольная точка этой прямой удовлетворяет уравнению конуса (4.33), действительно

Иначе говоря, поверхность конуса второго порядка состоит из прямых, проходящих через начало координат.

z

y

x

Рис. 44.

7. Поверхности вращения. Поверхность, образованная вращением линии вокруг оси, называется поверхностью вращения.

Пусть линия L лежит в плоскости Oxy, ее вращаем вокруг оси Ox. Уравнение линии

F (x, y) = 0. (4.35)

При вращении (рис. 45) , т. е. y в уравнении (4.35) перехо­дит в

Чтобы получить уравнение поверхности вращения линии вокруг оси Ox, следует в уравнение линии (4.35) вместо y подставить

y

x

z

P

B

Рис. 45.

A

j

L

y

Пример 14. Гипербола, лежащая в плоскости Oxz,

вращается относительно оси Oz. Найти уравнение полученной поверх­ности.

Решение. В уравнение гиперболы вместо x подставляя получаем уравнение однополостного гиперболоида вращения

Замечание. Путем преобразования системы координат (поворотом осей, симметричным отображением относительно координатных плоскостей, параллельным переносом) общее уравнение второго порядка

приводится к каноническому виду:

При этом уравнение поверхности (4.22) приводится к каноническому уравнению

· эллипсоида (мнимого эллипсоида),

· однополостного, двуполостного гиперболоида,

· эллиптического, гиперболического параболоида,

· конуса второго порядка,

· эллиптического, гиперболического, параболического цилиндра,

· пары параллельных или пересекающихся плоскостей (пары мнимых плоскостей).

Если в уравнение (4.22) , то уравнение (4.22) параллель­ным переносом осей координат приводится к каноническому виду.

Пример 15. Классифицировать поверхность, заданную уравне­нием

Решение.Выделим в уравнении полные квадраты:

С помощью преобразования системы координат (параллельного переноса) по формулам

получаем каноническое уравнение однополостного гиперболоида

Пример 16. Классифицировать поверхность, заданную уравне­нием

Решение. Выделим в уравнении полные квадраты:

С помощью преобразования системы координат (параллельного переноса) по формулам

получаем каноническое уравнение эллиптического параболоида

Пример 17. Классифицировать поверхность, заданную уравне­нием

Решение. Выделим в уравнении полные квадраты:

С помощью преобразования системы координат (параллельного переноса) по формулам

получаем уравнение пары пересекающихся плоскостей, параллельных оси Oz