Определители 2, 3 и n-го порядков (определения и их свойства). Теорема Лапласа о разложении определителя по элементам строки или столбца

Определители и их свойства

Понятие определителя - число, характеризующее квадратную матрицу 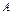, необходимо для решения систем линейных алгебраических уравнений.

Определитель матрицы 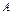обозначают , , .

1) Определителем матицы 1-го порядка 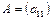, называется элемент : ;

2) Определителем матрицы 2-го порядка называется число, вычисляемое по формуле:

. Произведения называются членами определителя 2-го порядка.

Пример. Вычислить определитель матрицы . Р е ш е н и е. .

3) Определителем матрицы 3-го порядка называется число, вычисляемое по формуле:

.

Данная формула получила название правила треугольников или правило Сарруса.

При вычислении определителя 3-го порядка удобно пользоваться следующей схемой, показывающей произведения каких элементов берутся со знаком “+”, а каких со знаком “-“:

Пример. Вычислить определитель . Р е ш е н и е. .

4) Определитель квадратной матрицы -го порядка (определитель -го порядка).

Рассмотрим квадратную матрицу n -го порядка. Зачеркнем элемент матрицы, стоящий на пересечении 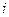-й строки и -го столбца. В результате получается матрица порядка . Пусть дана матрица 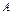n -го порядка:

.

Минором 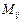элемента 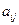матрицы n -го порядка называется определитель матрицы -го порядка, полученной из матрицы 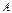вычеркиванием 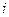-й строки и -го столбца.

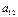Например минором матрицы 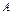3-го порядка будет:

Определение. Алгебраическим дополнением элемента матрицы 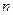-го порядка называется минор, взятый со знаком :

.

Пример. Найти алгебраические дополнения всех элементов матрицы

.

Р е ш е н и е:

,	,	,
,	,	,

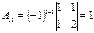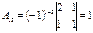Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:

(разложение по элементам 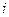-й строки; ).

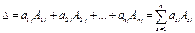
(разложение по элементам -го столбца; ).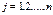

Пример. Вычислить определитель разложением по элементам

а) 1-й строки; б) 1-го столбца.

Р е ш е н и е. а) 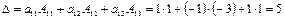, б) .