Отрезок прямой проецируется в натуральную величину лишь в том случае, когда он параллелен плоскости, на которую он проецируется

Во всех остальных случаях он проецируется наплоскостьпроекции с искажением.

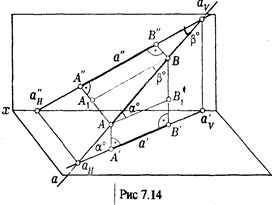
Для установления зависимости между действительной величиной отрезка прямой и его проекциями рассмотрим рис 7.14

99

В прямоугольной трапеции ABB'А' (углы при вершинах А¢ и В' — прямые) боковыми стор ими являются действительная величина отрезка [АВ] и его горизонтальная проекция [А¢ В¢ ], а основаниями [АА¢] и [ВВ¢ ] по величине равные удалению концов отрезка А и В от горизонтальной плоскости Н.

½АА¢ô=Z _(.)А;ôВВ¢ô=Z_(.)В

Через точку А, в плоскости трапеции, проводимАВ¢₁ôôА¢В¢, получим прямоугольный треугольник ABB¢₁, у которого катетАВ¢₁@[А¢В']. Поэтому геометрическая зависимость между действительной величиной отрезка и его горизонтальной проекцией может быть установлена с помощью прямоугольного треугольника, один из катетов которого равен горизонтальной проекции А¢ В¢, а другой - разности аппликат котлов отрезкаô BB¢ô-ô АА¢ô Гипотенуза этого треугольника /АВ/ равна действительной величине.

Зависимость между действительной величиной отрезка и его фронтальной проекцией также видна на чертеже.

Для графического определения на эпюре Монжа действительной величины отрезка достаточно построить прямоугольный треугольник, взяв за один его катет горизонтальную^ (фронтальную, профильную) проекцию отрезка, а за другой катет разность удаления концов отрезка от горизонтальной (или соответственно фронтальной, профильной) плоскости проекции.

На (рис 7.15) показано определение действительной величины ôАВô путем построения треугольника А¢В¢Во. На этом же чертеже приведен второй вариант решения задачи: построение треугольника А'"В "Ао на базе фронтальной проекции отрезка.

С помощью прямоугольного треугольника можно решать задачу по построению на эпюре проекции отрезка на перед заданной

длины.