Метод Ньютона

Рассмотрим систему n нелинейных уравнений с n неизвестными

или в векторной форме

f (x) = 0,

здесь .

Основная идея метода Ньютона состоит в выделении из уравнений системы линейных частей, которые являются главными при малых приращениях аргументов. Это позволяет свести исходную задачу к решению последовательности линейных систем [10].

Пусть известно некоторое приближение x ^(k) корня x*. Тогда поправку можно найти, решая систему

.

Для определения разложим векторную функцию 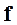в ряд по . Сохранив только линейные по части, получим

.

Здесь через 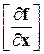обозначена матрица производных .

Если , то , где 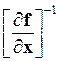- матрица, обратная матрице производных.

Таким образом, последовательные приближения корня можно вычислять по формуле

.

Отсюда видно, что метод Ньютона решения системы состоит в построении итерационной последовательности:

.

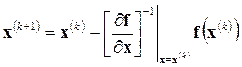Если , то в достаточно малой окрестности корня x* итерационный процесс сходится, причём с квадратичной скоростью, т.е. если , то . Поэтому в качестве критерия окончания итерационного процесса можно использовать условие . Если начальное приближение выбрано удачно, то метод Ньютона сходится очень быстро.