 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
А) ; б) ; в) ; г)
|
|
В задачах 141—150 даны функции y=f(x) и значения аргумента  и
и  . Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва; 3) построить график данной функции.
. Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва; 3) построить график данной функции.
141. 
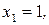

142. 


143. 


144. 


145. 


146. 


147. 


148. 


149. 


150. 


В задачах 151—160 функция у задана различными аналитическими выражениями для различных областей изменения аргумента х. Требуется: 1) найти точки разрыва функции, если они существуют; 2) определить характер разрыва; 3) сделать рисунок.
151. 

152. 

153. 

154. 

155. 

156. 

157. 

158. 

159. 

160. 

В задачах 161-180 определить производные  , пользуясь формулами дифференцирования.
, пользуясь формулами дифференцирования.
161. а)  б)
б)  в)
в)  г)
г)  д)
д) 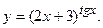
162. а)  б)
б)  в)
в)  г)
г)  д)
д) 
163. а)  б)
б)  в)
в)  г)
г)  д)
д) 
164. а)  б)
б)  в)
в)  г)
г)  д)
д) 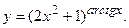
165. а)  б)
б)  в)
в)  г)
г)  д)
д) 
166. а)  б)
б)  в)
в) 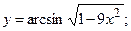 г)
г)  д)
д) 
167. а)  б)
б)  в)
в)  г)
г)  д)
д) 
168. а)  б)
б)  в)
в)  г)
г)  д)
д) 
169. а)  б)
б)  в)
в)  г)
г)  д)
д) 
170. а)  б)
б) 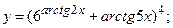 в)
в)  г)
г)  д)
д) 
171. а) 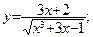 б)
б)  в)
в)  г)
г)  д)
д) 
172. а)  б)
б)  в)
в)  г)
г)  д)
д) 
173. а)  б)
б)  в)
в) 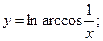 г)
г)  д)
д) 
174. а)  б)
б)  в)
в)  г)
г)  д)
д) 
175. а)  б)
б)  в)
в)  г)
г)  д)
д) 
176. а)  б)
б)  в)
в)  г)
г)  д)
д) 
177. а)  ; б)
; б)  в)
в)  ; г)
; г)  д)
д) 
178. а)  б)
б)  в)
в)  г)
г)  д)
д) 
179. а)  б)
б)  в)
в)  г)
г)  д)
д) 
180. а)  б)
б)  в)
в)  г)
г)  д)
д) 
В задачах 181—200 исследовать данные функции методами дифференциального исчисления и начертить их графики. Исследование и построение графика рекомендуется проводить по следующей схеме: 1) найти область существования функции; 2) исследовать функцию на непрерывность; найти точки разрыва функции и ее односторонние пределы в точках разрыва; 3) выяснить, не является ли данная функция четной, нечетной; 4) найти точки экстремума функции и определить интервалы возрастания и убывания функции; 5) найти точки перегиба графика функции и определить интервалы выпуклости и вогнутости графика функции; 6) найти асимптоты графика функции, если они имеются; 7) построить график функции, используя результаты исследования; при необходимости можно дополнительно находить точкиграфика, давая аргументу х ряд значений и вычисляя соответствующие значения у.
181. 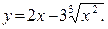
182. 
183. 
184. 
185. 
186. 
187. 
188. 
189. 
190. 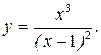
191. 
192. 
193. 
194. 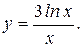
195. 
196. 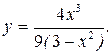
197. 
198. 
199. 
200. 
201. Требуется изготовить открытый сверху цилиндрический сосуд максимальной вместимости. Каковы должны быть размеры сосуда (радиус R и высота H), если на его изготовление имеется S=84,82дм2 материала
(S ≈ 27π)?
202. Требуется вырыть яму конической формы (воронку) с образующей а = 3 м. При какой глубине объем воронки будет наибольшим?
203. Найти высоту цилиндра наибольшего объема, который можно вписать в шар радиуса R?
204. В эллипс 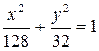 вписать прямоугольник наибольшей площади. Найти стороны этого прямоугольника, если они параллельны осям.
вписать прямоугольник наибольшей площади. Найти стороны этого прямоугольника, если они параллельны осям.
205. Требуется изготовить закрытый цилиндрический бак максимальной вместимости. Каковы должны быть размеры бака (радиус Rи высота H), если на его изготовление имеется S = 18,84 м2 материала (S ≈ 6π)?
206. В прямоугольной системе координат через точку М (2; 3) проведена прямая, которая вместе с осями координат образует треугольник, расположенный в первом квадранте. Каковы должны быть отрезки, отсекаемые прямой на осях координат, чтобы площадь треугольника была наименьшей?
207. Резервуар, открытый сверху, имеет форму прямоугольного параллелепипеда с квадратным основанием. Каковы должны быть размеры резервуара, чтобы на егo изготовление пошло наименьшее количество материала, если он должен вмещать 256 л воды?
208. Требуется вырыть яму цилиндрической формы с круглым основанием и вертикальной боковой поверхностью заданного объема V= 25 м2 ( V≈8π). Каковы должны быть линейные размеры ямы (радиус R и высота H), чтобы на облицовку ее дна и боковой поверхности пошло наименьшее количество материала?
209. Из круглого бревна радиуса R = 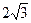 требуется вырезать балку прямоугольного сечения с основанием bи высотой h. Прочность балки пропорциональна bh2. При каких значениях bи hпрочность балки будет наибольшей?
требуется вырезать балку прямоугольного сечения с основанием bи высотой h. Прочность балки пропорциональна bh2. При каких значениях bи hпрочность балки будет наибольшей?
210. Требуется изготовить закрытый цилиндрический бак заданного объема V=50м3 ( V≈16π). Каковы должны быть размеры бака (радиус Rи высота H), чтобы на его изготовление пошло наименьшее количество материала?
211. Турист идет из пункта А, находящегося на шоссейной дороге, в пункт В, расположенный в 8 км от шоссе. Расстояние от А до В по прямой составляет 17 км. В каком месте туристу следует свернуть с шоссе, чтобы в кратчайшее время прийти в пункт В, если его скорость передвижения по шоссе 5 км/ч, а по бездорожью 3 км/ч?
212. Требуется поставить палатку в форме правильной четырехугольной пирамиды заданной боковой поверхности S = 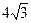 м2. Каковы должны быть размеры палатки (сторона основания а и высота H), чтобы вместимость палатки была наибольшей?
м2. Каковы должны быть размеры палатки (сторона основания а и высота H), чтобы вместимость палатки была наибольшей?
213. Равнобедренный треугольник, периметр которого Р = 12, вращается вокруг основания. Найти основание а, при котором полученное тело вращения имеет наибольший объем?
214. Цистерна имеет форму прямого кругового цилиндра, завершенного с одной стороны полушаром. Вместимость цистерны V=41,89м  (V≈
(V≈  π). Найти радиус цилиндра R, при котором цистерна будет иметь наименьшую полную поверхность.
π). Найти радиус цилиндра R, при котором цистерна будет иметь наименьшую полную поверхность.
215. Сечение оросительного канала имеет форму равнобочной трапеции, боковые стороны которой равны меньшему основанию. При каком угле наклона боковых сторон сечение канала будет иметь наибольшую площадь?
216. Требуется изготовить полотняный шатер, имеющий форму прямого кругового конуса заданной вместимости V=14,14м3 (V≈9/2π). Каковы должны быть размеры конуса (высота Hи радиус основания R ), чтобы на шатер ушло наименьшее количество полотна?
217. Сечение тоннеля имеет форму прямоугольника, завершенного сверху полукругом. Периметр сечения P=35,7м(P≈20+5π). При каком радиусе полукруга площадь сечения будет наибольшей?
218. Из прямоугольного листа жести размером 24 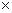 9 см требуется изготовить открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была наибольшей?
9 см требуется изготовить открытую сверху коробку, вырезая по углам листа равные квадраты и загибая оставшиеся боковые полосы под прямым углом. Каковы должны быть стороны вырезаемых квадратов, чтобы вместимость коробки была наибольшей?
219. Равнобедренный треугольник, вписанный в окружность радиуса R= 3, вращается вокруг основания. Найти высоту треугольника h, при котором полученное тело вращения имеет наибольший объем.
220. Найти высоту конуса наибольшего объема, который можно вписать в шар радиуса R.
В задачах 221–240 найти интегралы:
221. а)  ; б)
; б)  ; в)
; в)  .
.
222. а)  ; б)
; б)  ; в)
; в) 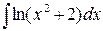 .
.
223. а)  ; б)
; б)  ; в)
; в)  .
.
224. а)  ; б)
; б)  ; в)
; в)  .
.
225. а)  ; б)
; б)  ; в)
; в) 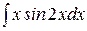 .
.
226. а)  ; б)
; б)  ; в)
; в)  .
.
227. а)  ; б)
; б)  ; в)
; в)  .
.
228. а)  ; б)
; б)  ; в)
; в)  .
.
229. а)  ; б)
; б)  ; в)
; в)  .
.
230. а)  ; б)
; б)  ; в)
; в)  .
.
231. а) 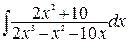 ; б)
; б)  ; в)
; в)  .
.
232. а) 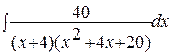 ; б)
; б)  ; в)
; в)  .
.
233. а)  ; б)
; б)  ; в)
; в)  .
.
234. а)  ; б)
; б)  ; в)
; в)  .
.
235. а) 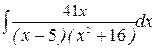 ; б)
; б)  ; в)
; в)  .
.
236. а)  ; б)
; б)  ; в)
; в)  .
.
237. а) 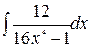 ; б)
; б)  ; в)
; в)  .
.
238. а)  ; б)
; б)  ; в)
; в)  .
.
239. а)  ; б)
; б) 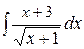 ; в)
; в)  .
.
240. а)  ; б)
; б)  ; в)
; в) 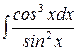 .
.
В задачах 241–260 вычислить определенные интегралы:
241. а)  ; б)
; б)  .
.
242. а) 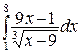 ; б)
; б)  .
.
243. а)  ; б)
; б)  .
.
244. а)  ; б)
; б)  .
.
245. а)  ; б)
; б)  .
.
246. а)  ; б)
; б)  .
.
247. а)  ; б)
; б) 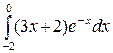 .
.
248. а)  ; б)
; б)  .
.
249. а)  ; б)
; б)  .
.
250. а) 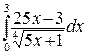 ; б)
; б)  .
.
251. а)  ; б)
; б) 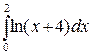 .
.
252. а)  ; б)
; б)  .
.
253. а)  ; б)
; б)  .
.
254. а)  ; б)
; б)  .
.
255. а)  ; б)
; б)  .
.
256. а)  ; б)
; б)  .
.
257. а)  ; б)
; б)  .
.
258. а)  ; б)
; б)  .
.
259. а)  ; б)
; б)  .
.
260. а)  ; б)
; б) 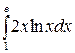 .
.
261.. Вычислить площадь фигуры, ограниченной параболами  и
и 
262. Вычислить площадь фигуры, ограниченной эллипсом 

263. Вычислить площадь фигуры, ограниченной астроидой 
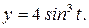
264. Найти объем тела, образованного вращением вокруг оси Ох фигуры, ограниченной параболой  прямой
прямой  и осью Оx.
и осью Оx.
265. Найти объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной гиперболой y=6/x,осью Оу и прямыми у = 1 и у = 6.
266. Найти объем тела, полученного вращением вокруг оси Ох эллипса x=acost, y=bsint.
267. Найти длину дуги кривой  от
от  до
до 
268. Найти длину дуги кривой  от
от  до
до 
269. Найти длину одной арки циклоиды x=a(t-sint), y=a(1-cost).
270. Найти длину кардиоиды ρ=2a(1-cosφ).
271. Найти площадь поверхности, образованной вращением вокруг оси Ох параболы  от
от  до
до 
272. Найти площадь поверхности, образованной вращением вокруг оси Ох астроиды 

273. Найти площадь поверхности, образованной вращением вокруг оси Ох одной арки циклоиды х = 3(t — sint), у = 3(1 — cos t ).
274. Найти площадь фигуры, ограниченной окружностями ρ =асоsφ и ρ =2а соsφ (а > 0).
275. Найти площадь фигуры, ограниченной кардиоидой ρ= 2(1- cosφ) и окружностью ρ = 2.
276. Найти координаты центра тяжести однородной плоской фигуры, ограниченной дугой синусоиды у= sinx и отрезком оси Ох от  до
до 
277. Найти координаты центра тяжести однородной плоской фигуры, ограниченной кривой  осью Ох и прямой х = 4.
осью Ох и прямой х = 4.
278. Найти координаты центра тяжести однородной плоской фигуры, ограниченной кривой  и осями координат.
и осями координат.
279. Найти координаты центра тяжести однородной плоской фигуры, ограниченной параболой  и прямой
и прямой 
280. Найти координаты центра тяжести однородной плоской фигуры, ограниченной эллипсом  и окружностью
и окружностью  и расположенной в первом квадранте.
и расположенной в первом квадранте.
В задачах 281– 300 вычислить несобственные интегралы или установить их расходимость.
281. 
282. 
283. 
284. 
285. 
286. 
287. 
288. 
289. 
290. 
291. 
292. 
293. 
294. 
295. 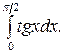
296. 
297. 
298. 
299. 
300. 
В задачах 301– 310 дана функция 
 . Найти: 1) полный дифференциал dz;
. Найти: 1) полный дифференциал dz;
2) частные производные второго порядка 
 и
и  ;
;
3) смешанные частные производные  и
и  .
.
301.  .
.
302. 
303. 
304. 
305. 
306. 
307. 
308. 
309. 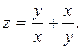
310..
311. Дана функция  . Показать, что
. Показать, что 
312. Дана функция  . Показать, что
. Показать, что 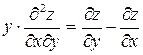 .
.
313. Дана функция  . Показать, что
. Показать, что 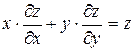 .
.
314. Дана функция  . Показать, что
. Показать, что 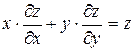 .
.
315. Дана функция  . Показать, что
. Показать, что  .
.
316. Дана функция  . Показать, что
. Показать, что  .
.
317. Дана функция  . Показать, что
. Показать, что  .
.
318. Дана функция  . Показать, что
. Показать, что  .
.
319. Дана функция  . Показать, что
. Показать, что  .
.
320. Дана функция 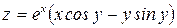 . Показать, что
. Показать, что  .
.
В задачах 321—330 найти наименьшее и наибольшее значения функции z=f(x, у) в заданной замкнутой области.
321.  в квадрате
в квадрате  .
.
322.  в треугольнике, ограниченном осями координат Оx и Oy и прямой
в треугольнике, ограниченном осями координат Оx и Oy и прямой  .
.
323.  в квадрате
в квадрате  .
.
324.  в квадрате
в квадрате  .
.
325.  в треугольнике, ограниченном осями координат Оx и Oy и прямой
в треугольнике, ограниченном осями координат Оx и Oy и прямой 
326.  в области, ограниченной параболой
в области, ограниченной параболой 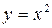 , осью Oy
, осью Oy  и прямой
и прямой  .
.
327.  в прямоугольнике
в прямоугольнике  .
.
328.  в области, ограниченной параболой
в области, ограниченной параболой  и осью Ox.
и осью Ox.
329. 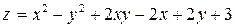 в треугольнике, ограниченном прямыми
в треугольнике, ограниченном прямыми  ,
,  ,
, 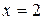 .
.
330.  в прямоугольнике
в прямоугольнике  .
.
В задачах 331–340 данную функцию z = f(x, у) исследовать на экстремум.
331. 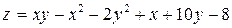 .
.
332. 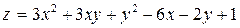 .
.
333. 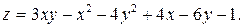
334.  .
.
335. 
336. 
337. 
338. 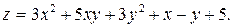
339. 
340. 
В задачах 341–360 требуется: 1) построить на плоскости хОу область интегрирования заданного интеграла; 2) изменить порядок интегрирования и вычислить площадь области при заданном и измененном порядках интегрирования.
341. 
342. 
343. 
344. 
345. 
346. 
347. 
348. 
349. 
350. 
351. 
352. 
353. 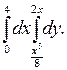
354. 
355. 
356. 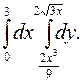
357. 
358. 
359. 
360. 
В задачах 361–380 вычислить объем тела, ограниченного указанными поверхностями. Данное тело и область интегрирования изобразить на чертеже.
361. 
362. 
363. 
364. 
365. 
366. 
367. 
368. 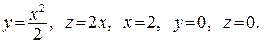
369. 
370. 
371. 
372. 
373. 
374. 
375. 
376. 
377. 
378. 
379. 
380. 
В задачах 381-390 исследовать сходимость рядов, пользуясь признаком сходимости Даламбера.
381. 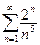 .
.
382.  .
.
383.  .
.
384.  .
.
385.  .
.
386.  .
.
387.  .
.
388.  .
.
389.  .
.
390.  .
.
В задачах 391-400 исследовать сходимость рядов, пользуясь интегральным признаком сходимости Коши.
391.  .
.
392.  .
.
393.  .
.
394.  .
.
395. 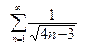 .
.
396.  .
.
397.  .
.
398. 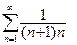 .
.
399.  .
.
400.  .
.
В задачах 401-420 дан степенной ряд  . Написать первые четыре члена ряда, найти интервал сходимости ряда и выяснить вопрос о сходимости ряда на концах интервала. Значения a, b и k даны.
. Написать первые четыре члена ряда, найти интервал сходимости ряда и выяснить вопрос о сходимости ряда на концах интервала. Значения a, b и k даны.
401. a = 2, b = 3, k = 4.
402. a = 6, b = 5, k = 3.
403. a = 3, b = 4, k = 5.
404. a = 5, b = 2, k = 4.
405. a = 4, b = 3, k = 3.
406. a = 2, b = 3, k = 5.
407. a = 5, b = 6, k = 2.
408. a = 3, b = 5, k = 6.
409. a = 3, b = 7, k = 3.
410. a = 2, b = 7, k = 3.
411. a = 5, b = 3, k = 4.
412. a = 4, b = 2, k = 2.
413. a = 7, b = 4, k = 5.
414. a = 2, b = 6, k = 3.
415. a = 4, b = 2, k = 4.
416. a = 6, b = 3, k = 5.
417. a = 5, b = 8, k = 6.
418. a = 4, b = 3, k = 2.
419. a = 2, b = 4, k = 7.
420. a = 3, b = 5, k = 3.
В задачах 421-440 требуется вычислить определенный интеграл с точностью до 0,001 путем предварительного разложения подынтегральной функции в ряд и почленного интегрирования этого ряда.
421.  .
.
422.  .
.
423.  .
.
424.  .
.
425.  .
.
426.  .
.
427.  .
.
428.  .
.
429.  .
.
430. 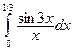 .
.
431.  .
.
432. 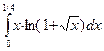 .
.
433. 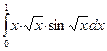 .
.
434.  .
.
435.  .
.
436.  .
.
437.  .
.
438.  .
.
439.  .
.
440.  .
.
В задачах 441-460 при указанных начальных условиях найти три первых (отличных от нуля) члена разложения в степенной ряд Маклорена функции у(х), являющейся частным решением дифференциального уравнения:
441.  .
.
442.  .
.
443.  .
.
444.  .
.
445.  .
.
446.  .
.
447.  .
.
448.  .
.
449.  .
.
450.  .
.
451.  .
.
452.  .
.
453.  .
.
454.  .
.
455.  .
.
456. 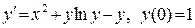 .
.
457.  .
.
458.  .
.
459.  .
.
460.  .
.
В задачах 461–470 найти общее решение (общий интеграл) дифференциальных уравнений первого порядка.
461..
462..
463..
464.
Дата публикования: 2014-11-04; Прочитано: 1687 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
