 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Тема 6 Производная и дифференциал
|
|
Пискунов, гл. III, § 1—3, упр. 1—4, 7—9; §4—8, упр. 10—25; §9, упр. 28, 30, 36, 39—47, 50; § 10, упр. 51—55, 60, 63, 66, 68—73, 79—85, 110—112; § 11, упр. 142—150; § 12—15, упр. 116—121, 127, 128; § 16—18, упр. 152—155; § 20—21, упр. 162—170; § 22—25, упр. 172, 173, 180, 195, 196, 201, 202, 204; § 26, упр. 207, 212, 214—216, 220.
Пискунов, гл. IV, § 1—3, упр. 1—7, 9, 10; § 4—5, упр. 18—30, 34— 36, 38—40; § 6—7, упр. 53—55.
Разберите решения задач 13 —17 из данного пособия.
Задача 13. Найти производные  следующих функций:
следующих функций:
а)  б)
б)  в)
в) 
г)  ; д)
; д)  ; е)
; е)  .
.
Решение: При нахождении производных функций используем правила дифференцирования и таблицу основных элементарных функций.
Правила дифференцирования:
1.  ;
;
2.  ;
;
3.  ;
;
4.  ;
;
5.  ;
;
6.  ;
;
7. 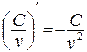 .
.
Таблица производных основных элементарных функций:
| Производные основных элементарных функций | Производные сложных функций |
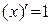
| 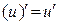
|

| 
|

| 
|

| 
|

| 
|

| 
|
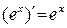
| 
|

| 
|

| 
|

| 
|

| 
|

| 
|

| 
|
| 
|

| 
|
а) Пользуясь правилом логарифмирования, корня и дроби, преобразуем правую часть:

Применяя правила и формулы дифференцирования, получим:

б) Предварительно прологарифмируем по основанию е обе части равенства:

Теперь дифференцируем обе части, считая 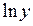 сложной функцией от переменной х:
сложной функцией от переменной х:
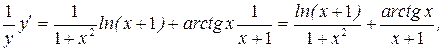
откуда
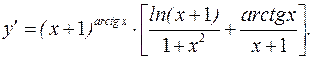
в) В данном случае зависимость между аргументом х и функцией у задана уравнением, которое не разрешено относительно функции у. Чтобы найти производную у', следует дифференцировать по х обе части заданного уравнения, считая при этом у функцией от х, азатем полученное уравнение решить относительно искомой производной у'. Имеем

Из полученного равенства, связывающего х, у и  находим производную у':
находим производную у':

откуда

г) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти искомую производную у', находим предварительно дифференциалы dy и dx и затем берем отношение этих дифференциалов

д) воспользуемся правилом дифференцирования частного, получаем: 






 .
.
е) Воспользуемся правилом дифференцирования сложной функции.

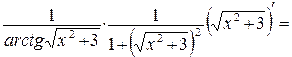


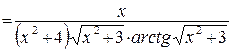 .
.
Задача 14. Найти производную второго порядка 
а)  б)
б) 
Решение: а) Функция у задана в неявном виде. Дифференцируем по х обе части заданного уравнения, считая при этом у функцией от х:
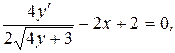 откуда
откуда 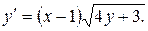 (1)
(1)
Снова дифференцируем по х обе части (1):
 (2)
(2)
Заменив у' в (2) правой частью (1), получим

б) Зависимость между переменными х и у задана параметрическими уравнениями. Чтобы найти производную у', находим сначала дифференциалы dy и dx, а затем берем их отношение:
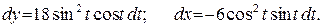
Тогда

Производная второго порядка 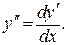 Следовательно, чтобы найти у", надо найти дифференциал dy':
Следовательно, чтобы найти у", надо найти дифференциал dy':

Тогда 
Задача 15. Найти приближенное значение функции
 при
при  , исходя из ее точного значения при х1 = 6.
, исходя из ее точного значения при х1 = 6.
Решение: Известно, что дифференциал dy функции y=f(x) представляет собой главную часть приращения этой функции 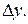 Если приращение аргумента
Если приращение аргумента  по абсолютной величине достаточно мало, то приращение
по абсолютной величине достаточно мало, то приращение  приближенно равно дифференциалу, т.е.
приближенно равно дифференциалу, т.е.  Так как
Так как  а
а  , то имеет место приближенное равенство:
, то имеет место приближенное равенство:

Пусть  , т.е.
, т.е.  .
.
Тогда 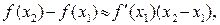
 (1)
(1)
Приближенное равенство (1) дает возможность найти значение функции при х=х2, если известно значение функции и ее производной при х = х1.
Прежде чем воспользоваться приближенным равенством (1), находим числовое значение производной у' при х = 6:

 или
или

Применяя (1), получим

Задача 16. Найти приближенное значение величины tg 47°.
Решение: Применяем формулу (1) задачи 15.
Рассмотрим функцию  . Дифференциал ее равен
. Дифференциал ее равен  Так как
Так как  то положим
то положим  и
и  Приращение
Приращение 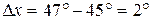 или в радианном измерении
или в радианном измерении  Следовательно,
Следовательно,
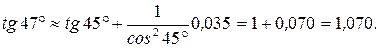
Задача 17. Дана парабола  и радиус окружности R= 10, центр которой находится в начале координат.
и радиус окружности R= 10, центр которой находится в начале координат.
Требуется: 1) найти точки пересечения параболы с окружностью; 2) составить уравнение касательной и нормали к параболе в точках ее пересечения с окружностью; 3) найти острые углы, образуемые кривыми в точках их пересечения.
Решение: 1) Уравнение окружности с центром в начале координат имеет вид:  , где R – радиус окружности. Следовательно,
, где R – радиус окружности. Следовательно,  есть уравнение данной окружности.
есть уравнение данной окружности.
Чтобы найти точки пересечения данных кривых, решаем совместно систему: 
В результате находим, что парабола и окружность пересекаются в двух точках: А(–8; –6) и В(8; –6) (рис. 7). 
2) Известно, что угловой коэффициент касательной к кривой у=f(x) в точке  лежащей на этой кривой, равен значению производной в точке касания, то есть
лежащей на этой кривой, равен значению производной в точке касания, то есть 
Для определения угловых коэффициентов касательных к параболе в точках А и В находим производную у':
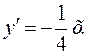 Следовательно,
Следовательно,  и
и 
Уравнение касательной к кривой  в точке
в точке  имеет вид
имеет вид
 (1)
(1)
Подставив в (1) координаты точки А и значение углового коэффициента  получим уравнение касательной к данной параболе в точке А:
получим уравнение касательной к данной параболе в точке А:

Подставив в (1) координаты точки В и  получим уравнение касательной к данной параболе в точке В:
получим уравнение касательной к данной параболе в точке В:

Прямая, проходящая через точку касания перпендикулярно к касательной, называется нормалью к кривой. Уравнение нормали к кривой у = f(x) в точке  имеет вид
имеет вид
 (2)
(2)
Подставив в (2) координаты точки А и kA = 2, находим уравнение нормали в точке А: х+2у+20 = 0. Аналогично находим уравнение нормали в точке В: х – 2у – 20 = 0.
3) Направление кривой в каждой ее точке определяется направлением касательной к ней в этой точке. Под углом между двумя кривыми в точке их пересечения понимается угол между касательными к этим кривым в рассматриваемой точке пересечения. Так как заданные кривые являются симметричными относительно оси ординат, то острые углы, образуемые данными кривыми в точках их пересечения, будут равны между собой. Поэтому достаточно найти угол между касательными к параболе и к окружности только в одной точке, например в точке А.
Определим угловой коэффициент  касательной АЕ, проведенной к окружности
касательной АЕ, проведенной к окружности  в точке А(– 8; – 6):
в точке А(– 8; – 6):

Из аналитической геометрии известно, что угол  между двумя прямыми определяется по формуле
между двумя прямыми определяется по формуле
 (3)
(3)
Положив в (3)  и
и  получим:
получим:

Таким образом, острый угол  , образуемый параболой и окружностью в точке пересечения А, составляет приближенно 63° 26'.
, образуемый параболой и окружностью в точке пересечения А, составляет приближенно 63° 26'.
Дата публикования: 2014-11-04; Прочитано: 1358 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
