Тема 2. Основы векторной алгебры

Ефимов, гл. 7-10. Минорский, № 390, 397, 399, 400, 405, 417, 418, 419, 427, 428, 434, 439, 440, 444. Разберите решение задачи 5 из данного пособия.

Задача 5. Даны координаты вершин пирамиды ABCD: A(2;1;0), B(3;-1;2), C(13;3;10), D(0;1;4). Требуется: 1) записать векторы и в системе орт и найти модули этих векторов; 2) найти угол между векторами и ; 3) найти проекцию вектора на вектор ; 4) найти площадь грани ABC; 5) найти объем пирамиды ABCD.

Решение:

1. Произвольный вектор может быть представлен в системе орт следующей формулой:

(1)

где а_х, а_у, а_z — проекции вектора на координатные оси Ох, Оу и Oz, a — единичные векторы, направле­ния которых совпадают с положительным направлением осей Ох, Оу и Oz.

Если даны точки то проекции вектора на координатные оси находятся по формулам:

. (2)

Тогда

(3)

Подставив в (3) координаты точек А и В, получим вектор:

.

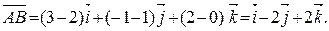Аналогично, подставляя в (3) координаты точек А и С, находим

.

Подставив в (3) координаты точек А и D,находим вектор

.

Если вектор 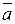задан формулой (1), то его модуль вычисляется по формуле

. (4)

Применяя (4), получим модули найденных векторов:

2. Косинус угла между двумя векторами равен ска­лярному произведению этих векторов, деленному на произведение их модулей:

Находим скалярное произведение векторов и по формуле:

.

Получаем

Модули этих векторов уже найдены: Следовательно,

3. Проекция вектора на вектор равна скалярному произведению этих векторов, деленному на модуль вектора :

4. Площадь грани ABCравна половине площади параллелограмма, построенного на векторах и . Площадь параллелограмма, построенного на векторах и , равна модулю векторного произведения векторов и . Вычислим векторное произведение по формуле: . Тогда значит

5. Объем параллелепипеда, построенного на трех некомпланарных векторах, равен абсолютной величине их смешанного произведения. Вычислим смешанное произведение 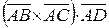по формуле: . Тогда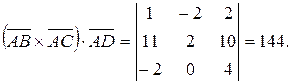

Следовательно, объем параллелепипеда равен 144 куб. ед., а объем заданной пирамиды ABCD: 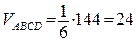куб. ед.