Уравнение Бернулли

Будем рассматривать идеальную несжимаемую жидкость, в которой внутреннее трение (вязкость) отсутствует. Выделим в стационарно текущей жидкости тонкую трубку тока (рис. 5.2) с сечениями S₁ и S₂, перпендикулярными к линиям тока. В сечении 1 за малое время t частицы сместятся на расстояние l₁, а в сечении 2 - на расстояние l₂. Через оба сечения за время t пройдут одинаковые малые объемы жидкости V = V₁ = V₂ и перенесут массу жидкости m=rV, где r - плотность жидкости. В целом изменение механической энергии всей жидкости в трубке тока между сечениями S₁ и S₂ , произошедшее за время t, можно заменить изменением энергии объема V, произошедшим при его перемещении от сечения 1 до сечения 2. При таком движении изменится кинетическая и потенциальная энергия этого объема, и полное изменение его энергии

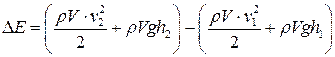, (5.2)

где v ₁ и v ₂ - скорости частичек жидкости в сечениях S₁ и S₂ соответственно; g - ускорение земного притяжения; h₁ и h₂ - высоты центра сечений.

В идеальной жидкости потери на трение отсутствуют, поэтому приращение энергии DE должно быть равно работе, совершаемой силами давления над выделенным объемом. При отсутствии сил трения эта работа:

. (5.3)

Приравнивая правые части равенств (5.2) и (5.3) и перенося члены с одинаковыми индексами в одну часть равенства, получим

. (5.4)

Сечения трубки S₁ и S₂ были взяты произвольно, поэтому можно утверждать, что в любом сечении трубки тока справедливо выражение

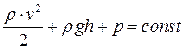. (5.5)

Уравнение (5.5) называется уравнением Бернулли. Для горизонтальной линии тока h = const, и равенство (5.4) приобретает вид

r 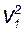/2 + p₁ = r· 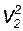/2 + p₂, (5.6)

т.е. давление оказывается меньшим в тех точках, где скорость больше.