Кинетическая энергия вращающегося твердого тела

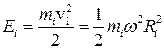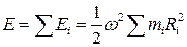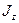1. Рассмотрим вращение тела вокруг неподвижной оси Z. Разобьем все тело на множество элементарных масс m _i. Линейная скорость элементарной массы m _i – v_i = w·R _i, где R _i – расстояние массы m _i от оси вращения. Следовательно, кинетическая энергия i -ой элементарной массы будет равна . Полная кинетическая энергия тела: , здесь – момент инерции тела относительно оси вращения.

Таким образом, кинетическая энергия тела, вращающегося относительно неподвижной оси равна:

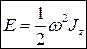(4.5)

2. Пусть теперь тело вращается относительно некоторой оси, а сама ось перемещается поступательно, оставаясь параллельной самой себе.

НАПРИМЕР: Катящийся без скольжения шар совершает вращательное движение, а центр тяжести его, через который проходит ось вращения (точка «О») перемещается поступательно (рис.4.17).

Скорость i -той элементарной массы тела равна , где 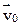– скорость некоторой точки «О» тела; 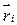– радиус-вектор, определяющий положение элементарной массы по отношению к точке «О».

Кинетическая энергия элементарной массы равна:

.

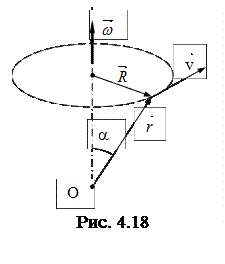
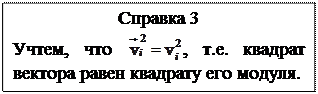ЗАМЕЧАНИЕ: векторное произведение 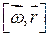совпадает по направлению с вектором и имеет модуль, равный 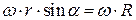(рис.4.18).

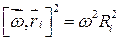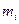Учтя это замечание, можно записать, что , где – расстояние массы от оси вращения. Во втором слагаемом сделаем циклическую перестановку сомножителей, после этого получим

.

Чтобы получить полную кинетическую энергию тела, просуммируем это выражение по всем элементарным массам, вынося постоянные множители за знак суммы. Получим

.

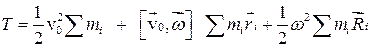Сумма элементарных масс 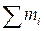есть масса тела «m». Выражение равно произведению массы тела на радиус-вектор 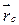центра инерции тела (по определению центра инерции). Наконец, 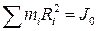– момент инерции тела относительно оси, проходящей через точку «О». Поэтому можно записать

.

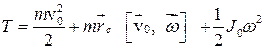Если в качестве точки «O» взять центр инерции тела «С», радиус-вектор 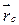будет равен нулю и второе слагаемое исчезнет. Тогда, обозначив через – скорость центра инерции, а через – момент инерции тела относительно оси, проходящей через точку «С», получим:

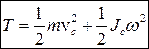(4.6)

Таким образом, кинетическая энергия тела при плоском движении слагается из энергии поступательного движения со скоростью, равной скорости центра инерции, и энергии вращения вокруг оси, проходящей через центр инерции тела.