 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Закон сохранения энергии
|
|
Без нарушения общности рассмотрим систему, состоящую из двух частиц массами m1 и m2. Пусть частицы взаимодействуют друг с другом с силами  и
и  , модули которых зависят от расстояния R12 между частицами. Установлено, что такие силы являются консервативными, т.е. работа, совершаемая такими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть также, кроме внутренних сил на первую частицу действует внешняя консервативная сила
, модули которых зависят от расстояния R12 между частицами. Установлено, что такие силы являются консервативными, т.е. работа, совершаемая такими силами над частицами, определяется начальной и конечной конфигурациями системы. Пусть также, кроме внутренних сил на первую частицу действует внешняя консервативная сила  и внешняя неконсервативная сила
и внешняя неконсервативная сила  . Аналогично для второй частицы. Тогда уравнения движения частиц можно записать в виде:
. Аналогично для второй частицы. Тогда уравнения движения частиц можно записать в виде:

Умножим каждое уравнение на  и сложим полученные выражения.
и сложим полученные выражения.
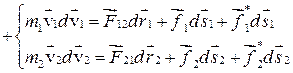

1. Распишем первый член в правой части.
Работа внутренних сил равна  . Для замкнутой системы
. Для замкнутой системы  , а
, а  , где
, где 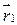 и
и  – радиус-векторы частиц.
– радиус-векторы частиц.
Тогда
 .
.
Учитывая, что силы  и
и  имеют величину, зависящую только от расстояния и направлены вдоль соединяющей их прямой (это справедливо, например, для сил кулоновского или гравитационного взаимодействий), любую из этих сил можно представить в виде, например,
имеют величину, зависящую только от расстояния и направлены вдоль соединяющей их прямой (это справедливо, например, для сил кулоновского или гравитационного взаимодействий), любую из этих сил можно представить в виде, например,  , где f(R 12 ) – некоторая функция R 12,
, где f(R 12 ) – некоторая функция R 12,  – орт вектора
– орт вектора  .
.
Следовательно,  .
.
Скалярное произведение  равно приращению dR 12 расстояния между частицами, тогда
равно приращению dR 12 расстояния между частицами, тогда  .
.
Выражение  есть приращение некоторой функции
есть приращение некоторой функции 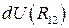 . Следовательно,
. Следовательно,
 .
.
Функция 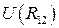 представляет потенциальную энергию взаимодействия.
представляет потенциальную энергию взаимодействия.
Работа внутренних сил будет равна
 ,
,
т.е. не зависит от пути, по которому перемещаются частицы, а определяется начальной и конечной конфигурациями системы. Т.е. силы взаимодействия вида  являются консервативными.
являются консервативными.
Итак, работа внутренних сил равна убыли потенциальной энергии взаимодействия

2. Второй член представляет работу внешних сил и равен убыли потенциальной энергии системы во внешнем поле консервативных сил

3. Последний член представляет работу неконсервативных внешних сил  .
.
После этих замечаний можно записать

Величина
T + Uвз. + Uвн. = E (3.13)
– называется полной механической энергией системы. Если внешние неконсервативные силы отсутствуют, т.е.  , то
, то
Е=const – закон сохранения механической энергии.
ОПРЕДЕЛЕНИЕ: полная механическая энергия системы тел, на которые действуют лишь консервативные силы, остается постоянной.
Для замкнутой системы, т.е. системы, на тела которой не действуют никакие внешние силы, закон сохранения примет вид:
E = T + Uвз. = const
Если в замкнутой системе, кроме консервативных сил действуют неконсервативные силы, например, силы трения, то полная механическая энергия системы не сохраняется. Рассматривая консервативные силы как внешние, получим

или после интегрирования  .
.
| Как правило, силы трения совершают отрицательную работу. Поэтому наличие сил трения в замкнутой системе приводит к уменьшению ее полной механической энергии со временем. Таким образом, если в системе действуют неконсервативные силы, то | |

| изменение полной энергии будет равно работе всех внешних сил, действующих на эту систему. |
Анализ закона сохранения показывает, что полная энергия, оставаясь в консервативной системе величиной постоянной, может переходить из одних видов в другие.
При действии неконсервативных сил возможен переход механической энергии в другие немеханические виды энергии. В этом случае справедлив более общий закон сохранения:
ОПРЕДЕЛЕНИЕ: в изолированной от любых внешних воздействий системе остается постоянной сумма всех видов энергии (включая и немеханические).
К этому добавим, что в природе и технике постоянно имеют место превращения энергии из одних видов в другие. Проиллюстрируем это таблицей.
| Процесс или прибор | Превращение энергии | |
| из вида | в вид | |
| Электрогенератор | механическая | электрическая |
| Гальванический элемент | химическая | электрическая |
| Электродвигатель | электрическая | механическая |
| Зарядка аккумулятора | электрическая | химическая |
| Фотосинтез | электромагнитная | химическая |
| Фотоэффект | электромагнитная | электрическая |
| Ядерный реактор | ядерная | механическая электромагнитная и др. |
 В таблице не отражено, что при любом превращении часть энергии превращается в теплоту.
В таблице не отражено, что при любом превращении часть энергии превращается в теплоту.
Для графического изображения закона сохранения энергии рассмотрим случай, когда тело бросаем вверх.
Если не учитывать силу сопротивления воздуха Fсопр., то систему «тело-Земля» можно рассматривать, как изолированную и консервативную, для которой
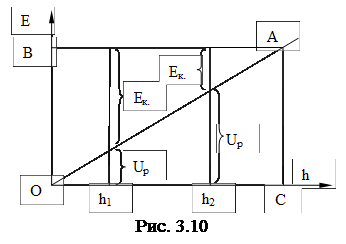
E = Eк. + Up. = const
Из графика (рис. 3.10) видно, что по мере поднятия тела над поверхностью Земли его потенциальная энергия возрастает от величины Up(h1) до Up(h2), но одновременно с этим точно на такую же величину уменьшается кинетическая энергия системы Eк., а полная энергия тела остается величиной постоянной, что соответствует линии BA || h.
Очевидно:
1. При h=0 имеем Up=0, а E=Eк., что соответствует линии ОВ;
2. При h = max имеем Up = max (Eк. = 0), а E = Up, что соответствует линии AC.
САМОСТОЯТЕЛЬНО:
Упругий и неупругий центральный удар шаров;
Условия равновесия механической системы.
Дата публикования: 2014-11-04; Прочитано: 989 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
