Работа, совершаемая при перемещении контура с током в магнитном поле

Рассмотрим отрезок проводника с током, способный свободно перемещаться по двум направляющим во внешнем магнитном поле (рис.9.5). Магнитное поле будем считать однородным и направленным под углом α по отношению к нормали к плоскости перемещения проводника.

ds

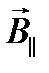
Рис.9.5. Отрезок проводника с током в однородном магнитном поле.

Как видно из рис.9.5, вектор имеет две составляющие и , из которых только составляющая 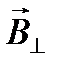создает силу, действующую в плоскости перемещения проводника. По абсолютной величине эта сила равна:

,

где I – сила тока в проводнике; l – длина проводника; B – индукция магнитного поля.

Работа этой силы на элементарном пути перемещения ds есть:

.

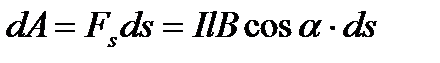Произведение lds равно площади dS, заметанной проводником при движении, а величина BdScosα равна потоку магнитной индукции dФ через эту площадь. Следовательно, можем написать:

dA=IdФ.

Рассматривая отрезок проводника с током как часть замкнутого контура и интегрируя это соотношение, найдем работу при перемещении контура с током в магнитном поле:

A = I(Ф₂ – Ф₁)

где Ф₁ и Ф₂ обозначают поток индукции магнитного поля через площадь контура соответственно в начальном и конечном положениях.