 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Примеры вычисления магнитных полей с помощью закона Био-Савара-Лапласа
|
|
1) Напряженность магнитного поля в центре кругового витка с током.
В данном случае имеем, согласно закону Био-Савара-Лапласа (рис.8.6):
,
откуда находим после интегрирования по всей длине витка – окружности радиуса R:
. 
. 
Рис.8.6. Магнитное поле в центре кругового витка с током.
2) Отрезок проводника с током конечной длины и бесконечно длинный проводник с током
В этом случае имеем (рис.8.7):
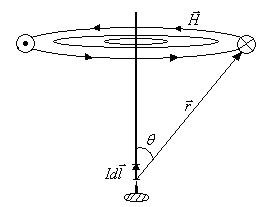
Рис.8.7. Магнитное поле прямолинейного проводника с током.
,
где
, 
, 
,
тогда
.
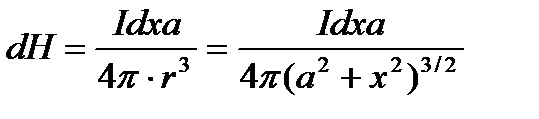Интегрируя это выражение в пределах от – x1 до x2, находим:
где 
.
Переходя в этой формуле к пределу при 
и 
, получим формулу для расчета напряженности магнитного поля прямолинейного проводника с током бесконечной длины:
.
3) Магнитное поле движущегося заряда.
Любой проводник с током создает в окружающем пространстве магнитное поле. Но ток в проводнике – есть направленное движение зарядов. Следовательно, можно допустить, что источником магнитного поля являются движущиеся заряды. Тогда магнитное поле, созданное проводником с током в некоторой точке пространства, будет представлять собой суперпозицию магнитных полей, созданных в этой же точке пространства каждым из движущихся зарядов в отдельности.
Пусть 
– скорость упорядоченного движения зарядов в проводнике; q – заряд носителя тока (в металлах q = - e). Для элемента тока можем написать:
dNq 
,
где n = dN/dV – концентрация зарядов, dN – число зарядов в элементе объема dV = Sdl.
На основании закона Био-Савара-Лапласа, напряженность магнитного поля, созданного одним движущимся зарядом, будет:
или в векторном виде
.
Эта формула отражает релятивистскую (относительную) сущность магнитного поля. Она показывает, что магнитное поле проявляется как результат относительного движения заряда. Отметим, что приведенная формула справедлива при скоростях движения заряда 
(с=3∙108 м/с – скорость света в вакууме).
Дата публикования: 2014-11-04; Прочитано: 1233 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
