Магнитное поле на оси кругового витка с током

Согласно закону Био-Савара-Лапласа, индукция магнитного поля, создаваемого элементом тока dl на расстоянии r от него есть

,

где α – угол между элементом тока и радиус-вектором , проведенным из этого элемента в точку наблюдения; r - расстояние от элемента тока до точки наблюдения.

В нашем случае α = π/2, sin α = 1; , где а – расстояние, отсчитываемое от центра витка до рассматриваемой точки на оси витка. Векторы 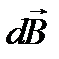образуют в этой точке конус с углом раствора при вершине 2 = π - 2β, где β – угол между отрезками а и r.

Из соображений симметрии ясно, что результирующее магнитное поле на оси витка будет направлено вдоль этой оси, то есть вклад в него дают только те составляющие, которые параллельны оси витка:

.

Результирующую величину индукции магнитного поля B на оси витка получим, проинтегрировав это выражение по длине контура от 0 до 2πR:

или, подставив значение r:

.

В частности, при а = 0 находим индукцию магнитного поля в центре кругового витка с током:

Этой формуле можно придать другой вид, воспользовавшись определением магнитного момента витка с током:

.

Последнюю формулу можно записать в векторном виде (см. рис.9.1):

.