Вычисление координат точек теодолитного хода

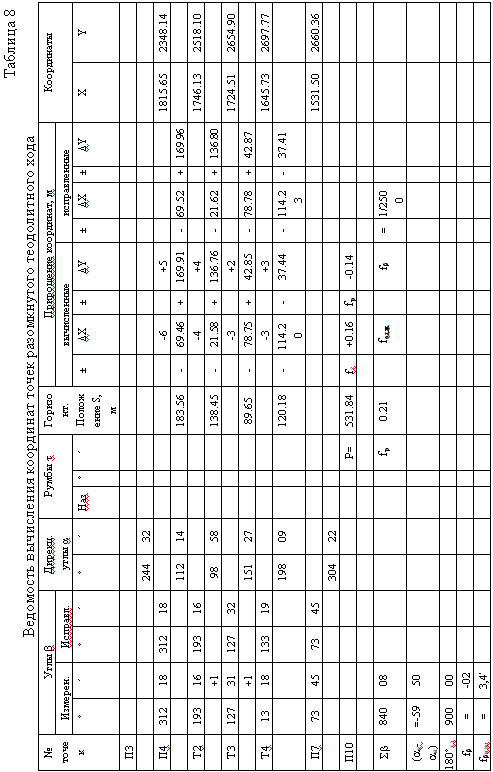
После измерения углов и длин линий сразу же приступают к вычислению координат точек хода, так как при этом производится окончательный контроль измерений. Вычисления выполняются в специальной ведомости, образец которой для вычисления координат замкнутого хода приведен в табл. 7, а для разомкнутого хода − в табл. 8. В ведомостях через строку выписываются следующие данные: номера точек в соответствии с их обозначениями на схемах (см. рис. 8, 9); координаты исходных пунктов (П6, П4, П7), на которые опираются ходы; дирекционные углы исходных направлений (α_П7-П6, α_П3-П4, α_П7-П10), измеренные значения горизонтальных углов β и горизонтальные проложения S -линий.

Вычисления выполняются в следующем порядке.

1. Уравнивание (увязка) углов. Вначале вычисляется угловая невязка. Для замкнутого хода используется формула

, (13)

где β_i − измеренные внутренние углы замкнутого полигона; n − число вершин полигона.

Для разомкнутого хода угловая невязка вычисляется по формулам

, (14)

если измерены правые по ходу углы, или

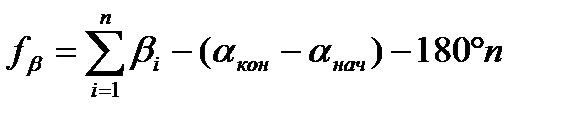, (15)

если измерены левые по ходу углы, где 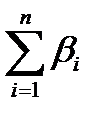− сумма измеренных углов; a_нач − дирекционный угол начальной стороны хода; a_кон − дирекционный угол конечной стороны хода; n - количество измеренных углов.

Угловая невязка является показателем точности измерения углов. Она сравнивается с величиной предельной невязки, которая подсчитывается по формуле

, (16)

где t − точность отсчетного приспособления теодолита (t = l);

n − количество измеренных углов. Если |f_b|£f_bпред, то невязка f_b распределяется. Для этого в значения измеренных углов вводятся поправки со знаком, обратным знаку невязки. Невязка распределяется либо поровну во все измеренные углы, либо (для упрощения дальнейших вычислений) − путем введения поправок в углы, образованные наиболее короткими сторонами. В последнем случае величины поправок берут равными 0,5'. Поправки выписываются над измеренными углами (табл. 7, 8).

Далее вычисляются исправленные значения углов

b_испр= b_изм+n_b. (17)

Если |f_b|>f_bпред, то проверяются вычисления углов в журнале, правильность вычисления величины невязки f_b Если при этом ошибка не будет обнаружена, то углы следует измерить заново.

2. Вычисление дирекционных углов линий хода выполняется по формулам

a_посл= a_пред ±180°- b_испр, (18)

если измерены правые углы, и

a_посл= a_пред ±180° + b_испр, (19)

если измерены левые углы

где a_посл − дирекционный угол последующей линии хода; a_пред − дирекционный угол предыдущей линии хода; b_испр − исправленный угол между ними.

При вычислении дирекционных углов замкнутого хода в качестве исходного принимается дирекционный угол a_П6-Т2 (см. рис. 9) первой линии хода, который в данном случае может быть вычислен по формуле

a_П6-Т2 = a_П7-П6 ±180° + b₀, (20)

где a_П7-П6 − дирекционный угол стороны П7-П6 опорной сети, значение которого известно; b₀ − примычный угол (левый по ходу).

Если в районе работ нет пунктов опорной геодезической сети, то дирекционный угол первой стороны замкнутого хода определяется по измеренному значению магнитного азимута А_Т1-Т2.

Контроль вычисления дирекционных углов для замкнутого хода производится путем повторного вычисления дирекционного угла первой линии хода П6-Т2 по дирекционному углу последней линии, например, для рис. 9:

a_П6-Т2 = a_Т4-П6 ±180° + b_1испр , (21)

а для разомкнутого хода в получении дирекционного угла a_кон (a_П7-П10 на рис. 10).

3. Вычисление приращений координат производится по формулам

D х = S cosa (22)

D y = S cosa

где S и a, − соответственно горизонтальное проложение и дирекционный угол линии хода. Если вычисления производятся на микрокалькуляторе, то значения D х, D y будут выданы с нужными знаками. Поэтому нет необходимости вычислять румбы. Однако не следует забывать превращать минуты в доли градуса при вычислении значений тригонометрических функций.

4. Линейная невязка, контроль точности линейных измерений.

Координатные невязки в замкнутом ходе вычисляются по формулам: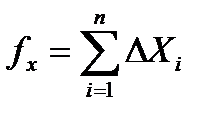

(23)

где n - число сторон в ходе.

В разомкнутом ходе они будут:

(24)

где х _н, y _н и х _к, y _к − координаты соответственно начальной и конечной точек хода.

Линейная абсолютная невязка хода (невязка в периметре) вычисляется по формуле

(25)

и является критерием точности измерения длин линий. Для этого обычно вычисляется относительная невязка в виде простой дроби

, (26)

где − периметр хода.

Если f _отн > 1/2000, то следует проверить вычисления приращений координат, невязок. Если при этом ошибка не будет найдена, то длины линий необходимо измерить заново. Здесь 1/2000 − величина относительной ошибки измерения длин линий мерной лентой для средних условий местности.

При f _отн < 1/2000 приступают к уравниванию приращений координат.

5. Уравнивание приращений координат. Координатные невязки f_x, f_y распределяются прямо пропорционально длинам линий хода. Для этого вычисляются поправки

(27)

где S_i − длины линий; P − периметр хода; i= 1, 2…72;n − число сторон в ходе. Поправки имеют знак, обратный знаку невязки, и вычисляются с округлением до сантиметра. Для упрощения вычислений в формулах (27) величины f_x, f_y следует брать в сантиметрах, а Р и S − в сотнях метров (например, при S = 251,38 м следует брать S = 2,5).

После вычисления поправок выполняется контроль:

(28)

Равенства (28) могут не выполняться вследствие ошибок округлений на 1−2 см. Поэтому одну − две поправки следует исправить на 1 см. Поправки выписывают в ведомости вычисления координат в сантиметрах над соответствующими приращениями (см. табл. 7, 8).

Исправленные приращения вычисляют по формулам

D х _испр=D х _выч+n_{D х}

D y _испр=Dy_выч+n_Dy (29)

5. Вычисление координат точек теодолитного хода выполняется по формулам

х _посл= х _пред+D х _испр

y _посл= y _пред+D y _испр (30)

где х _пред, y _пред − координаты предыдущей точки, х _посл, y _посл − координаты последующей точки хода; D х _испр, D y _испр − исправленные приращения координат между этими точками.

Если замкнутый теодолитный ход не содержит пункта опорной геодезической сети, то координаты первой его точки задаются условно.

Контроль правильности вычисления координат точек и исправленных приращений заключается в повторном вычислении координат начальной точки (замкнутый ход) и конечной точки (разомкнутый ход), записанных в последней строке ведомости.