Определители второго порядка

Пусть дана квадратная матрица второго порядка

.

ОПРЕДЕЛЕНИЕ 3.1. Определителем второго порядка, соответствующим заданной матрице А, называется число, равное .

Для обозначения определителя используются вертикальные черточки и прописная буква D. Например,

(5)

есть общий вид определителя второго порядка.

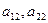Числа называются элементами определителя. Как и у матрицы второго порядка, элементы образуют первую строку определителя; - вторую строку; - первый столбец; - второй столбец; - образуют главную диагональ определителя; - побочную диагональ. Используя данную терминологию, можно сказать, что определитель второго порядка есть число, равное разности произведений элементов, расположенных на главной и побочной его диагоналях.

ПРИМЕР 3.1. .

Рассмотрим простейшие свойства определителя второго порядка.

Свойство 3.1. определитель не изменится, если его строки поменять местами с соответствующими столбцами, т.е.

(6)

Действительно, согласно (5) получим

и .

Из свойства 3.1 следует, что свойства, установленные для строк определителя, справедливы и для его столбцов.

Свойство 3.2. При перестановке местами двух строк (столбцов) определитель меняет свой знак на противоположный.

Действительно, если , то .

Свойство 3.3. Определитель, имеющий две одинаковые строки (столбца), равен нулю.

Например, .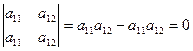

Свойство 3.4. Если все элементы какой-либо строки (столбца) определителя умножить на одно и то же число, то определитель умножится на это число.

Пусть , где k – число.

Тогда .

Свойство 3.4 означает, что общий множитель всех элементов строки (столбца) можно вынести за знак определителя.

Свойство 3.5. Определитель, у которого элементы двух его строк (столбцов) пропорциональны, равен нулю.

Действительно, при любом k.

Свойство 3.6. Если каждый элемент какой-либо строки (столбца) определителя есть сумма двух слагаемых, то определитель равен сумме двух определители, у одного из них элементами соответствующей строки являются первые слагаемые, у другого – вторые. Оставшиеся элементы этих определителей те же, что и у данного.

Пусть .

Тогда .

Свойство 3.7. Определитель не изменится, если к элементам какой-либо его строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на одно и тоже число.

Действительно, пусть .

Тогда, согласно свойствам 3.5 и3.6 получим

.