Умножение матриц

Пусть заданы матрица А размеров 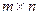и матрица в размеров , т.е. такие, что число столбцов первой равно числу строк второй матрицы. Выберем строку с номером i из матрицы А и столбец с номером j из матрицы В. умножим каждый элемент выбранной строки на соответствующий элемент выбранного столбца и сложим полученные произведения, т.е. составим сумму

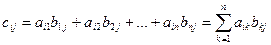. (4)

Вычислим такие суммы для всех и всех и из полученных чисел составим матрицу .

Произведением матрицы А размеров 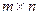на матрицу В размеров называется матрица размеров , элементы которой определяются по формуле (4) для всех и всех .

ПРИМЕР 2.1. Даны и .

Так как число столбцов матрицы А равно числу строк матрицы В, то произведение определено и

.

ПРИМЕР 2.2. Даны , .

Матрица А имеет два столбца, В – две строки; следовательно, определено:

.

ПРИМЕР 2.3. Даны квадратная матрица А порядка n и столбцовая матрица В размеров .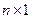

.

Из примера следует, что произведение квадратной матрицы на матрицу-столбец есть матрица-столбец. Аналогично проверяется, что произведение матрицы-строки размеров 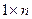на квадратную матрицу порядка n есть строчная матрица размеров .

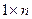ПРИМЕР 2.4. Даны , .

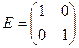и

.

Итак, если Е единичная матрица и А – квадратная, то , т.е. единичная матрица играет роль единицы в действиях над матрицами.

ПРИМЕР 2.5. Даны

Очевидно, что определены произведения и .

Этот пример показывает, что произведение двух матриц не подчиняется переместительному закону, т.е. . Однако можно проверить, что умножение матриц подчиняется сочетательному и распределительному законам, т.е. и .