Структурные средние величины

Для изучения структуры вариационных рядов исчисляются мода и медиана.

Под модой в статистике понимается вариант, который наиболее часто встречается в вариационном ряду. Модой будет то значение, которое имеет наибольшую частоту.

В интервальном ряду мода исчисляется по формуле:

где Xm₀ – нижняя граница модального интервала;

i – величина модального интервала;

f_m – частота модального интервала;

f_m-1 – частота предмодального интервала;

f_m-1 – частота послемодального интервала;

Медианой в статистике называется значение признака у той единицы совокупности, которая расположена в середине упорядоченного ряда. При нечетном числе вариантов, порядковый номер варианта, которому соответствует медиана, исчисляется по формуле:

где N – номер;

Если число вариантов ряда четное, то медиана будет расположена между:

n	и	n+2

В интервальном ряду медианой является значение признака у той единицы совокупности, которая делит вариационный ряд по сумме частот на 2 равные части так, что у половины единиц значения признака меньше медианы, а у второй половины – больше ее и рассчитывается медиана по формуле:

где х_mе – нижняя граница медианного интервала

i – величина медианного интервала;

∑f – сумма частот;

f_mе – частота медианного интервала;

S_mе-1 – сумма накопленных частот до медианного интервала.

5.4 Показатели вариации: порядок расчета и практическое применение

Условия, в которых находится каждый из изучаемых объектов, их социальные, экономические и прочие особенности развития выражаются конкретными числовыми уровнями статистических показателей. Таким образом, вариация, т.е. одновременное несовпадение уровней одного и того же явления или признака у разных единиц совокупности, носит объективный характер и помогает познать сущность и причины этого явления.

Для измерения вариации применяют несколько способов. Наиболее простым является расчет показателя размаха вариации R как разности максимального (Хmax) и минимального (Xmin) значений признака:

R = Хmax – Xmin

Преимущество показателя размаха вариации — наглядность и простота расчета. Однако эта характеристика учитывает лишь крайние — может быть, совершенно случайные значения признака.

Более полными оценками вариации являются общие характеристики отклонений от среднего уровня признака. Самый простой показатель такого типа — среднее линейное отклонение (или среднее абсолютное отклонение) – это среднее арифметическое значение абсолютных отклонений признака от его среднего уровня:

Среднее линейное отклонение простое:

Среднее линейное отклонение взвешенное:

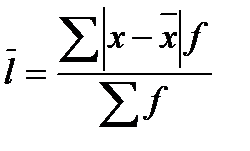
Показатель линейного отклонения широко применяется на практике. С его помощью изучаются, например, ритмичность и равномерность производства, равномерность поставок материалов и отгрузки готовой продукции, разрабатываются системы материального стимулирования и т.д. Однако этот показатель усложняет вероятностные расчеты, затрудняет применение методов математической статистики. Поэтому в статистических исследованиях для измерения вариации чаще применяют показатель отклонения от среднего уровня в форме дисперсии.

Дисперсия признака определяется на основе квадратической средней и обозначается σ².

Дисперсия простая:

Дисперсия взвешенная:

Средний квадрат отклонения представляет собой корень квадратный из дисперсии. Он характеризует среднюю колеблемость признака совокупности.

Средний квадрат отклонения простой:

Средний квадрат отклонения взвешенный:

Показатель дисперсии в статистике является оценкой одноименного показателя теории вероятностей и (как сумма квадратов отклонений) оценкой показателя дисперсии в математической статистике, что и позволяет использовать положения этих теоретических дисциплин для анализа социально-экономических процессов. Характеристика вариации уровнем дисперсии или средним квадратическим отклонением используется в корреляционном анализе — для оценки связи статистических переменных, в регрессионном анализе — для определения типов и параметров этих связей, и дисперсионном анализе — для обнаружения основных причин из­менения уровня результативного показателя, а также весьма широко в многомерных статистических методах.

Для взаимного сравнения и сопоставления уровня вариации разных признаков вариацию представляют в относительной форме. Относительные показатели вариации определяются делением абсолютного уровня вариации признака на его среднее значение. Соответственно получают:

– для размаха вариации — коэффициент осцилляции;

– для среднего линейного отклонения — относительное линейное отклонение;

– для среднего квадратического отклонения – коэффициент вариации.

Коэффициент вариации характеризует относительную колеблемость признака в совокупности и представляет собой отношение среднего квадратического отклонения к средней арифметической. Он позволяет сравнивать вариацию непосредственно несопоставимых показателей и рассчитывается по формуле: