 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Виды средних величин, порядок их вычисления
|
|
Все средние величины делятся на два больших класса:
1) степенные средние; к ним относятся такие известные и часто применяемые виды, как средняя арифметическая величина, средняя квадратическая и средняя геометрическая;
2) структурные средние величины, в качестве которых рассматриваются мода и медиана.
Средняя арифметическая бывает простой и взвешенной.
Средняя арифметическая простая применяется в тех случаях, когда отдельные значения осредняемого признака встречаются в совокупности один или одинаковое число раз. Она равна сумме всех индивидуальных значений, поделенной на их число.
Средняя арифметическая простая рассчитывается по формуле:
| _ х= | х1 + х2 + х3 + … + хn | = | ∑х |
| n | n |
_
где х – средняя арифметическая;
х1,2,3… – отдельные значения осредняемого признака (варианты);
n – число индивидуальных величин.
Средняя арифметическая взвешенная применяется в тех случаях, когда отдельные значения осредняемого признака встречаются в совокупности не одинаковое число раз. Она равна сумме произведения всех индивидуальных значений, помноженных на частоты, и поделенной на сумму частот:
| _ х= | х1f1 + х2f2 + х3f3 + … + хnfn | = | ∑хf |
| f1 + f2 + f3 + … + fn | ∑f |
где f – частота, показывающая, сколько раз повторяется тот или иной признак.
В ряде случаев осредняемый признак представлен не конкретными данными, а в виде интервалов. Чтобы перейти от интервальных значений к конкретным, используется серединное значение интервала, которое определяется суммированием верхних и нижних границ интервала и делением этой суммы пополам.
Если не известны нижняя граница первого интервала и верхняя граница последнего интервала, то используют величину, интервала, рядом с ними расположенного.
В практике статистики бывают случаи, когда весами являются производные признаки, представляющие собой произведения индивидуальных значений на частоты. Например, имеются данные об общем заработке и средней зарплате одного рабочего, а количество рабочих не известно.
В этих случаях применяется формула средней гармонической, которая представляет собой обратную величину средней арифметической, исчисленной из обратных значений осредняемого признака.
Средняя гармоническая простая:
| _ хгарм= | = | n | ||||
| + | +…+ | ∑ | ||||
| х1 | х2 | хn | х | |||
| n |
Средняя гармоническая взвешенная применяется в случаях, если веса отдельных значений не одинаковы
Средняя гармоническая взвешенная:
| _ хгарм= | = | = | ∑w | ||||||||
| w1 | + | w2 | +…+ | wn | ∑ | w | ∑ | w | |||
| х1 | х2 | хn | x | x | |||||||
| w1 + w2 + … + wn | ∑w |
где w – веса
Средняя геометрическая применяется в тех случаях, когда необходимо исчислить средние темпы изменения явления во времени.
Средняя геометрическая:

где Х1,2,3 – цепные коэффициенты роста
n – число коэффициентов роста
П – произведение
Средняя квадратическая применяется в тех случаях, когда осредняемый признак представлен линейными мерами, например, для определения средних расстояний или среднего диаметра труб и т.д.
Средняя квадратическая простая:

Средняя квадратическая взвешенная:
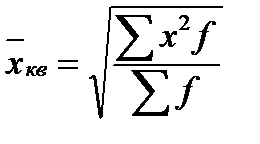
Дата публикования: 2015-11-01; Прочитано: 1498 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
