П. 4. Проективная плоскость

1. Проективная плоскость. Проективная геометрия — раздел геометрии, изучающий проективные свойства фигур, свойтсва, не меняющиеся при проектировании. Это такие свойства, как коллинеарность точек, т.е. принадлежность их одной прямой, и порядок алгебраической кривой. Эта геометрия возникла при научном обосновании перспективы в живописи.

При проектировании одной плоскости на другую точки плоскости могут уйти в бесконечность. Поэтому проективная плоскость получается из обычной эвклидовой дополнением последней бесконечно удаленными точками, образующими бесконечно удаленную прямую. Итак, проективная плоскость — замкнутая односторонняя поверхность, что и отражено в таблице. При разрезе проективная плоскость превращается в лист Мёбиуса.

Проективную плоскость можно склеить из квадрата (см. рис.), как тор и бутылку Клейна. Сначала деформируем квадрат, превратив его в поверхность шара без четырехугольника ABCD. Теперь склеим AB с CD и DA с BC так, чтобы совпали точки A с C и B с D. Для этого приподнимем точки A и C и опустим точки B и D. Получим замкнутую поверхность с линией самопересечения в виде отрезка, топологическую эквивалентную проективной плоскости.

2. Классификация. Рассмотренные выше топологические свойства не изменяются при гомеоморфизме поверхностей и называются топологиче­скими инвариантами. Сведем их в одну таблицу.

Поверхность	Изображение	Склеивание из квадрата	Число сторон	Число краев	Связ­ность	Хроматическое число и карта раскраски
Квадрат							1 2
Кольцо							1 2
Сфера							1 2
Тор							4 5 3 4 2 1 2 6 7 6 4 5 3 4
Лист Мёбиуса							1 2 3 4 5 2 6 1
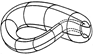
Бутылка Клейна							1 2 3 5 6
Проективная плоскость							1 2 3 5 6