Дифференциальные уравнения. Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям

Задача 30.

Найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям:

30.1. .

30.2. , y (0) = 3.

30.3. , y (0) =3.

30.4. .

30.5. , y (0) = –1.

30.6. .

30.7. , y (1) = 2.

30.8. .

30.9. .

30.10. .

Задача 31.

Решить дифференциальное уравнение второго порядка:

31.1 ; 31.2. ;

31.3. 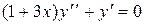; 31. 4. ;

31.5. ; 31.6. ;

31.7. 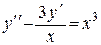; 31.8. ;

31.9. ; 31.10. .

Задача 32.

Методом Эйлера решить систему линейных однородных дифференциальных уравнений:

32.1 32.2.

32.3. 32.4.

32.5. 32.6.

32. 7. 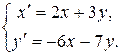32.8.

32.9. 32.10.

Задача 33.

Решить методом исключения систему линейных неоднородных дифференциальных уравнений:

7. Ряды

Задача 34.

Исследовать сходимость числового ряда (в случае знакопеременного ряда - исследовать на абсолютную сходимость)

34.1. а)	б)
34.2.а)	б)
34.3.а)	б)
34.4.а)	б)
34.5.а)	б)
34.6.а)	б)
34.7.а)	б)
34.8.а)	б)
34.9.а)	б)
34.10.а)	б)

Задача 35.

Найти область сходимости степенного ряда.

35.1.	35.6.
35.2.	35.7.
35.3.	35.8.
35.4. 35.5.	35.9 35.10

Задача 36.

Записать ряд Тейлора для функции f (x) в точке х ₀. Найти радиус и интервал сходимости полученного ряда.

36.1. 36.2. 36.3. f (x) = 2–3 x , х 0 = 1 36.4. 36.5

36.6 f (x) = 31– x, х 0 = 2 36.7. 36.8. 36.9. f (x) = 4–3 – 2 x, х 0 = –1 36.10.

Задача 37.

Вычислить интеграл с точностью до 0,001, разложив подынтегральную функцию в ряд:

37.1. 37.2. 37.3. 37.4. 37.5.

37.6. 37.7. 37.8. 37.9. 37.10.

Задача 38.

Разложить в ряд Фурье функцию, заданную графически:

38.1.

38. 2.
38.3.
38.4.
38.5.
38.6.
38.7.
38.8.
38.9.
38.10.

Заключение

Вы успешно провели решение заданий для контроля знаний студентов. Изученные и выполненные вами задания по дисциплине «Математика» способствуют углубленному изучению предмета «Математика» и существенно облегчают учебную деятельность студентов направления 220700.62 «Автоматизация технологических процессов и производств».

Задания для контроля знаний существенно помогают студентам приобрести устойчивые навыки решения основных программных задач дисциплины.

Структурно-логическое построение заданий для контроля знаний позволяет читателю проследить и понять связи между различными модулями дисциплины «Математика» и усвоить ключевые положения этого курса и подготовиться к заключительному контролю по дисциплине.

Вы закончили изучение дисциплины «Математика» – основной фундаментальной дисциплины инженерно-технической подготовки молодых специалистов.

Содержание

Введение ……………………………………………………………………... Содержание контрольных работ…………………………………………… Задания для контрольных работ…………………………………………… 1. Алгебра и геометрия…………………………………………………. 2. Введение в математический анализ………….……………………… 3. Дифференциальное исчисление функции одной переменной…….. 4. Функции нескольких переменных…………………………………… 5. Интегральное исчисление функции одной и нескольких переменных……………………………………………………………. 6. Дифференциальные уравнения………………………………………. 7. Ряды………………………………………………………………..... Заключение …………………………………………………………….......... Содержание ……………………………………………………………..........

С.Ф.Яковлева, Т.Н.Логиновская, О.М.Беличенко, М.Н.Слива

Математика

задания для контроля знаний

студентов направления 220700.62

«Автоматизация технологических процессов и производств»

__________________________________________________________________

Изд. №

__________________________________________________________________