 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Функции нескольких переменных
|
|
Задача 18.
Найти область определения функции. Сделать чертеж.
18.1. а)  ; б)
; б)  .
.
18.2.. а)  ; б)
; б)  .
.
18.3.. а)  ; б)
; б)  .
.
18.4. а)  ; б)
; б)  .
.
18.5. а)  ; б)
; б)  .
.
18.6. а)  ; б)
; б)  .
.
18.7. а)  ; б)
; б)  .
.
18.8. а)  ; б)
; б)  .
.
18.9. а)  ; б)
; б) 
18.10. а)  ; б)
; б)  .
.
Задача 19.
Проверить, удовлетворяет ли данная функция  указанному уравнению.
указанному уравнению.
19.1  ,
, 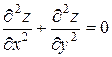 .
.
19.2  ,
,  .
.
19.3  ,
, 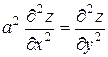 .
.
19.4  ,
,  .
.
19.5 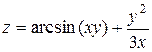 ,
, 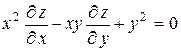 .
.
19.6  ,
,  .
.
19.7  ,
,  .
.
19.8.  ,
, 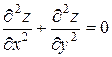 .
.
19.9  ,
,  .
.
19.10.  ,
, 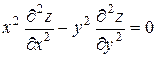
Задача 20.
Линеаризовать функцию  в окрестности точки
в окрестности точки  .
.
20.1. 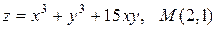 .
.
20.2. 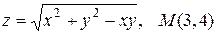 .
.
20.3.  .
.
20.4.  .
.
20.5.  .
.
20.6. 
20.7.  .
.
20.8.  .
.
20.9.  .
.
30.10.  .
.
Задача 21.
Для функции  найти:
найти:
а) производную в точке  в направлении вектора
в направлении вектора  ;
;
б) градиент в точке  и наибольшую скорость изменения функции в этой точке.
и наибольшую скорость изменения функции в этой точке.
21.1.  .
.
21.2.  .
.
21.3. 
 .
.
21.4..  .
.
21.5.  .
.
21.6.  .
.
21.7. 
 .
.
21.8. 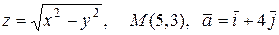 .
.
21.9.  .
.
21.0.  .
.
Задача 22.
Найти экстремум функции  .
.
22.1.  .
.
22.2.  .
.
22.3.  .
.
22.4.  .
.
22.5.  .
.
22.6. 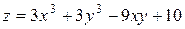 .
.
22.7. 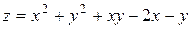 .
.
22.8.  .
.
22.9.  .
.
22.10. 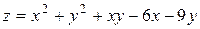 .
.
Задача 23.
Методом наименьших квадратов найти функцию y = f (x) в виде y = ax + b (в нечетных номерах) и y = ax 2 + b (в четных номерах). Экспериментально полученные п значений искомой функции y = f (x) при п значениях аргумента приведены в таблице.
23.1. 
23.2. 
23.3. 
23.4. 
23.5. 
23.6. 
23.7. 
23.8. 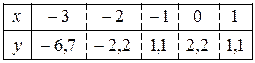
23.9. 
23.10. 
Интегральное исчисление функций одной и нескольких
Переменных
Задача 24
Найти неопределенный интеграл. В пунктах  и
и  результат проверить дифференцированием.
результат проверить дифференцированием.
24.1.  
|  
|
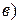 
|  
|
24.2.  
|  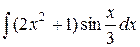
|
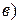 
|  
|
24.3.  
|  
|
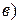 
|  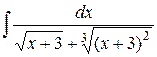
|
24.4.  
|  
|
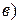 
|  
|
24.5.  
|  
|
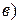 
|  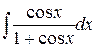
|
24.6.  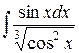
|  
|
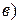 
|  
|
24.7.  
|  
|
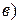 
|  
|
24.8.  
|  
|
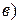 
|  
|
24.9.  
|  
|
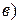 
|  
|
24.10.  
|  
|
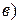 
|  
|
Задача 25
Пользуясь формулой Ньютона-Лейбница, вычислить определенный интеграл:
25.1.  
|  
|
25.2.  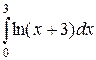
|  
|
25.3.  
|  
|
25.4.  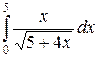
|  
|
25.5.  
|  
|
25.6.  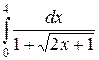
|  
|
25.7.  
|  
|
25.8.  
|  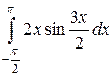
|
25.9.  
|  
|
25.10.  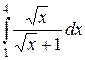
|  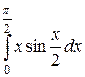
|
Задача 26
Сделать чертеж и с помощью определенного интеграла вычислить:
26.1. Площадь фигуры, ограниченной линиями  и
и 
 .
.
26.2. Площадь фигуры, ограниченной линиями  ,
, 
 ,
, 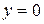 .
.
26.3. Площадь фигуры, ограниченной линиями  и
и  .
.
26.4. Площадь фигуры, ограниченной линиями  ,
, 
 ,
,  ,
,  .
.
26.5. Объём тела, образованного вращением вокруг оси  фигуры, ограниченной линиями
фигуры, ограниченной линиями  и
и  .
.
26.6. Объём тела, образованного вращением вокруг оси  фигуры, ограниченной линиями
фигуры, ограниченной линиями  и
и  .
.
26.7. Объём тела, образованного вращением вокруг оси  фигуры, ограниченной линиями
фигуры, ограниченной линиями  и
и  .
.
26.8. Длину дуги линии  от
от  до
до  .
.
26.9. Длину дуги одной арки циклоиды  ,
, 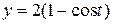 .
.
26.10. Длину дуги линии  от
от  до
до  .
.
Задача 27
Вычислить несобственный интеграл или установить его расходимость:
27.1. 
| 27.2. 
|
27.3. 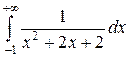
| 27.4. 
|
27.5. 
| 27.6. 
|
27.7. 
| 27.8. 
|
27.9. 
| 27.10. 
|
Задача 28
С помощью двойного интеграла найти объем тела, ограниченного данными поверхностями. Построить данное тело и область интегрирования:
28.1. 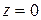 ,
,  ,
,  .
.
28.2. 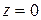 ,
, 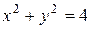 ,
,  .
.
28.3. 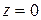 ,
,  ,
, 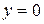 ,
,  ,
,  .
.
28.4. 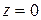 ,
, 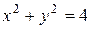 ,
,  .
.
28.5. 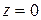 ,
,  ,
,  .
.
28.6. 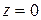 ,
,  ,
,  .
.
28.7. 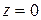 ,
,  ,
,  .
.
28.8. 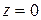 ,
,  ,
, 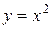 .
.
28.9. 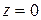 ,
,  ,
,  .
.
28.10. 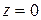 ,
,  ,
, 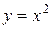 .
.
Задача 29
С помощью криволинейного интеграла второго рода найти работу силы  при перемещении материальной точки вдоль заданного пути
при перемещении материальной точки вдоль заданного пути  :
:
29.1.  ,если
,если  -дуга эллипса
-дуга эллипса  (
(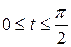 ).
).
29.2.  ,если
,если  -дуга астроиды
-дуга астроиды  (
(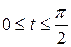 ).
).
29.3.  ,если
,если  -дуга линии
-дуга линии  (
(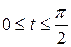 ).
).
29.4.  ,если
,если  -дуга линии
-дуга линии 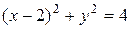 (
( ).
).
29.5.  ,если
,если  -дуга астроиды
-дуга астроиды  (
( ).
).
29.6.  ,если
,если  -дуга линии
-дуга линии  от т.
от т.  до т.
до т.  .
.
29.7.  ,если
,если  -дуга линии
-дуга линии  (
( ).
).
29.8.  ,если
,если  -дуга линии
-дуга линии  (
( ).
).
29.9.  ,если
,если  -дуга линии
-дуга линии  (
( ).
).
29.10.  ,если
,если  -дуга линии
-дуга линии 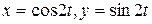 (
(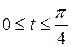 ).
).
Дата публикования: 2015-11-01; Прочитано: 439 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
