Основные законы распределения

Дискретная случайная величина имеет биномиальный закон распределения с параметрами и , если она принимает значения 0, 1, 2, … ,…, с вероятностями, определяемыми формулой Бернулли:

, (24)

где .

Если случайная величина распределена по биномиальному закону, то она имеет математическое ожидание и дисперсию , где .

Мода случайной величины , как целое число находится из неравенств:

.

Дискретная случайная величина имеет закон распределения Пуассона с параметром , если она принимает значения 0, 1, 2,…, ,… (бесконечное, но счетное множество значений) с вероятностями:

, (25)

где функция Пуассона.

Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру этого закона

. (26)

Дискретная случайная величина имеет геометрическое распределение с параметром , если она принимает значения 1, 2, …, ,…(бесконечное, но счетное множество значений) с вероятностями:

, (27)

где .

Если случайная величина имеет геометрическое распределение, то ее математическое ожидание ,а дисперсия .

Случайная величина , имеющая геометрическое распределение, представляет собой число испытаний, проведенных по схеме Бернулли, с вероятностью наступления события в каждом испытании до первого положительного исхода.

Дискретная случайная величина имеет распределение Паскаля с параметрами и , если она принимает значения с вероятностями:

. (28)

Ее числовые характеристики

, .

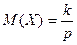Геометрическое распределение является частным случаем распределения Паскаля для .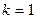

Распределение Паскаля характеризует число испытаний в схеме Бернулли до го положительного исхода.

Пример 32. Вероятность выигрыша по облигациям займа за все время их действия равна 0,1. Составить закон распределения числа выигрышных облигаций среди 5 приобретенных. Найти математическое ожидание, дисперсию и моду этой случайной величины. Вычислить математическое ожидание и дисперсию доли выигрышных облигаций среди приобретенных.

Решение. Пусть число выигрышных облигаций среди 5 приобретенных. Эта дискретная случайная величина, которая имеет биномиальное распределение с параметрами 5, 0,1. Значения от 0 до 5 принимаются с вероятностями, находимыми по формуле (24):

0,59049;

0,32805;

0,0729;

0,0081;

0,00045;

0,00001.

Контроль: 0,59049+0,32805+0,0729+0,0081+0,00045+0,00001=1.

Отсюда ряд распределения имеет вид:

	0,59049	0,32805	0,0729	0,0081	0,00045	0,00001

Определяем числовые характеристики , имеющей биномиальное распределение:

0,5; 0,45.

Доля выигрышных облигаций среди приобретенных есть , где случайная величина, распределенная по биномиальному закону.

Поэтому

0,1;

0,018.

Пример 33. Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа элемента в течение времени равна 0,002. Необходимо:

1. Составить закон распределения отказавших за время элементов;

2. Найти и этой случайной величины;

3. Определить вероятность того, что за время откажет хотя бы один элемент.

Решение. 1. Имеем схему Бернулли при 0,002 и 1000. Так как мало, а - велико, и при этом

,

то можно считать, что число отказавших за время элементов имеет распределение Пуассона, которое является предельным для биномиального распределения.

Тогда закон распределения числа отказавших элементов задается формулой (25):

.

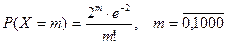2. Числовые характеристики найдем по формулам (26)

2.

3. События «откажет хотя бы один элемент» () и «отказов не будет» () являются противоположными, поэтому

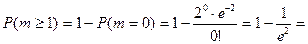0,865.

Пример 34. Экзаменатор задает студенту дополнительные вопросы. Вероятность того, что студент ответит на любой заданный вопрос, равна 0,9. Преподаватель прекращает экзамен, как только студент обнаруживает незнание заданного вопроса.

Требуется:

1. Составить закон распределения числа дополнительных вопросов, которые преподаватель задаст студенту.

2. Найти и этой случайной величины.

3. Найти наивероятнейшее число дополнительных вопросов.

Решение.

1. Пусть число дополнительных вопросов. Это дискретная случайная величина, которая принимает целые значения: 1, 2, 3,…, ,…. Найдем вероятности этих событий.

Событие (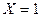) произойдет тогда, когда студент не ответит на первый же дополнительный вопрос. Вероятность этого равна 1-0,9=0,1, т. е.

0,1.

, если студент ответит на первый вопрос (с вероятностью 0,9) и не ответит на второй (с вероятностью 0,1). Отсюда по теореме умножения вероятностей

.

, если студент ответит на два дополнительных вопроса (с вероятностью ) и не ответит на третий вопрос (с вероятностью 0,1). Тогда

.

Нетрудно по аналогии получить, что событие () произойдет с вероятностью

.

Из последней формулы видно, что случайная величина имеет геометрическое распределение (27) с параметром 0,1.

Поэтому ряд распределения имеет вид:

				…		…
	0,1	0,09	0,081	…		…

2. Математическое ожидание и дисперсия случайной величины, имеющей геометрическое распределение, находятся по формулам:

10; 90.

3. Наивероятнейшее число дополнительных вопросов характеризуется модой случайной величины. Из ряда распределения видно, что

1.

Пример 35. Решить пример 34 при условии, что экзаменатор задает дополнительные вопросы до неправильного ответа на два вопроса.

Решение. Обозначим через число заданных вопросов до двух неверных ответов. Тогда является дискретной случайной величиной с возможными значениями: 2, 3, 4,…, ,…. Определим вероятности этих событий.

Событие () произойдет в том случае, когда студент не ответит на два дополнительных вопроса подряд. Это произойдет с вероятностью

.

Событие () совершится только в двух случаях: либо студент правильно ответит на первый вопрос и не ответит на два последующих, либо он не ответит на первый вопрос, затем правильно ответит на второй вопрос и не ответит на третий вопрос. Поскольку эти случаи несовместны, то вероятность события определится

.

Случайная величина примет значение 4 в трех случаях:

- студент правильно отвечает на первые два вопроса, но не отвечает на два последующих;

- студент правильно отвечает на первый и третий вопрос, но не отвечает на второй и четвертый;

- студент не отвечает на первый вопрос, затем правильно отвечает на второй и третий вопросы, но не отвечает на четвертый вопрос.

Тогда

.

Отсюда несложно получить общую формулу для вычисления вероятности события ():

.

Из последней формулы видно, что случайная величина имеет распределение Паскаля (28) с параметрами 0,1 и 2.

Поэтому числовые характеристики найдутся:

20, 180.

По определению моды должны выполняться неравенства:

,

,

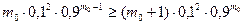которые после упрощения записываются в виде

,

.

Решая последнюю систему неравенств, получаем

.

Поскольку мода – целое число, то имеем бимодальную случайную величину: 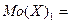9 и 10.

При этом 0,0387.